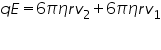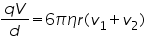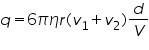| . | . | |||
| . | Millikan's oil drop experiment |
. | ||
| . |
Aim
Apparatus
Millikan’s oil drop apparatus,oil, Dc supply.
Construction Oil drop experiment was performed originally by the American physicist Robert A. Millikan in 1909. It measures the size of charge on a single electron.
Apparatus consist of an atomizer, which helps to spray tiny droplets. By means of a short focal distance telescope, the droplets can be viewed. There are two plates, one positive and the other negative above and below the bottom chamber.dc supply is attached to the plates. Some of the oil drops fall through the hole in the upper plate.
Theory
Initially the oil drops are allowed to fall between the plates in the absence of electric field. Due to gravity they accelerate first, but gradually slowdown because of air resistance.
The terminal velocity v1 in the absence of an electric field is calculated as
where 'l1' is the distance travelled by the oil drop and ’t1’ is the time taken.
The drag force acting upon the drop is calculated from stokes’s law and is given as
The apparent weight (true weight minus up thrust) for a perfectly spherical body is given by,
FV-FG=0. i.e., r-radius of oil drop
where V is the balancing potential and d is the distance between the plates.
If the applied electric force Fe is greater than the downward forces, some of the drops (the charged ones) will start to rise. Now the electric force will act upwards,gravity and viscous forces acts downwards. Corresponding terminal velocity v2 is calculated as,
Now the total force acting on drop is Fe-F’v-FG=0. Fe=F’v+FG
F'V is the new viscous force under the action of electric field. Millikan repeated the experiment no. of times, each time varying the strength of X-rays ionizing the air. As a result no. of electrons attaching to the oil drop varied. Then he obtained various values for q, and is found to be a multiple of 1.6 x 10-19C.
Cite this Simulator: |
..... | ||
| ..... | ..... | |||
 |
Copyright @ 2024 Under the NME ICT initiative of MHRD |
 |


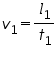
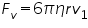
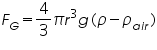
 At terminal velocity the oil drop is not accelerating, so the total force acting on it must be zero
At terminal velocity the oil drop is not accelerating, so the total force acting on it must be zero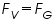
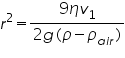
 If the electric forces Fe, balances the gravitational force FG, the drop suspends in the air.
If the electric forces Fe, balances the gravitational force FG, the drop suspends in the air.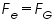
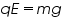
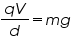
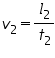
 where l2 is the distance travelled by the oil drop and t2 the time taken.
where l2 is the distance travelled by the oil drop and t2 the time taken.