
| . | you are here->home->Chemical Sciences->Physical Chemistry Virtual Lab-> Verification of Tafel Equation |
. | ||
| . | Verification of Tafel Equation |
. | ||
| . |
Objective:
Introduction:
Tafel's name is an adjective in the language of all trained electrochemists, yet not too many of them would even know his first name. The fame of the "Tafel law" and "Tafel line" overshadow Tafel's claim to fame as one of the founders of modern electrochemistry.
Until 1893, Tafel had lectured organic chemistry, but after 1893 he lectured physical and general chemistry. By German tradition, this would include lots of electrochemistry, and lots of experimentation. With strychnine reduction, Tafel had truly turned electrochemist. A careful observer, Tafel soon was able to summarize his major and rather far-reaching general deductions from his experimental work.
Professor Julius Tafel, around 1905.
Theory:
Tafel equation and Tafel plots
Tafel equation governs the irreversible behaviour of an electrode. To understand this we can consider the general mechanism of electron transfer to an electrode. Consider an electrolyte in which an inert or noble electrode is kept immersed. It is called working electrode, (
At the thermodynamic equilibrium of the system no net current flows across
Where
The equilibrium mentioned above is dynamic. Though no net current flows across the electrodes, both reduction and oxidation takes place at equal rate, so that the composition of the electrolyte does not change. The dynamic flow of electrons or charge in both directions can be written in terms of current densities as follows.
Negative to Positive to
The famous Butler-Volmer equation is expressed as: From this equation, it can be understand that the measured current density is a function of (i) over potential ( (ii) exchange current density ( (iii) anodic and cathodic transfer coefficients ( Transfer coefficients are not independent variables. In general, For many reaction, Equation (4) indicates that the current density at any over potential is the sum of cathodic and anodic current densities. At the extreme condition of over potential being highly negative, cathodic current density increases while anodic current density becomes negligible. At this stage, the first term in Butler-Volmer equation (4) becomes negligible. The equation can be written as:
Equation 7 is called Cathodic Tafel equation. Similarly at positive over potentials higher than 52 mV, anodic current density is much higher than cathodic and the cathodic current density becomes negligible. Hence
Equation (9) is called Anodic Tafel equation.
Experimental Determination of I and Tafel Plot
The test electrode is kept immersed in its salt solution. The solution should be very dilute so that the concentration near the surface of the electrode does not differ too much from the bulk concentration. A calomel electrode is kept very close to the test electrode. An inert electrode is also taken which serves as the counter electrode. A DC potential is applied across the test and the counter electrodes, making the test electrode negative. This establishes a potential across the test and the reference electrodes which is read by a very sensitive voltmeter connected in the circuit. From this value the rest potential is subtracted to get the applied potential component on the test electrode. An ammeter connected in series reads the current passing through the circuit. The applied potential is increased which increases the over potential on the cathode (test electrode is made more negative) and the corresponding current value is measured (ammeter reading). In this way the current values are taken for several over potential values making test electrode more and more negative. The log values of these current values are plotted against the over potential on one side.
Significance of Tafel Plots
As cathodic transfer coefficient value increases reduction is favoured and oxidation is not favoured and vice versa for anodic transfer coefficient. The transfer coefficients depend on the pH of the medium; in acidic conditions (low pH) reduction is favoured which is revealed by an increase in
Cite this Simulator: |
..... | ||
| ..... | ..... | |||
 |
Copyright @ 2024 Under the NME ICT initiative of MHRD |
 |


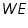 ). Also assume that an oxidised and a reduced species are present near the electrode and exhibit the following electron transfer reaction.
). Also assume that an oxidised and a reduced species are present near the electrode and exhibit the following electron transfer reaction. 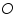 is the oxidised and
is the oxidised and 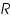 is the reduced species present at equilibrium and is stable in the solution. Let us assume that no other electron transfer reaction other than the above occurs. Let the concentration of
is the reduced species present at equilibrium and is stable in the solution. Let us assume that no other electron transfer reaction other than the above occurs. Let the concentration of 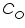 and
and 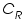 respectively and they are very low. An inert electrolyte is also present to minimise IR drop. Along with
respectively and they are very low. An inert electrolyte is also present to minimise IR drop. Along with 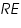 is also kept immersed, to form the cell. Since the potential of
is also kept immersed, to form the cell. Since the potential of 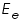 , which according to Nernst equation is,
, which according to Nernst equation is,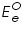 is the standard or formal reversible potential and is constant.
is the standard or formal reversible potential and is constant. ![Double click to edit «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfenced close=¨]¨ open=¨[¨»«mrow»«msub»«mi»C«/mi»«mi»O«/mi»«/msub»«mo»/«/mo»«msub»«mi»C«/mi»«mi»R«/mi»«/msub»«/mrow»«/mfenced»«/math»](/fckeditor/editor/plugins/fckeditor_wiris/integration/showimage.php?formula=aedaf18999baeafb992fbffc5dd944a5.png) . The square bracketed term should be in terms of activity rather than molar concentration; but at low concentration the replacement is error free.
. The square bracketed term should be in terms of activity rather than molar concentration; but at low concentration the replacement is error free. 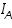 is anodic and
is anodic and 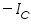 is cathodic current densities. By convention, anodic current density is given +ve sign and cathodic -ve sign.
is cathodic current densities. By convention, anodic current density is given +ve sign and cathodic -ve sign. 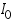 is known as exchange current density. It may be defined, as "the flow of charge or electrons across an electrochemical system in equilibrium". Its value normally is very low, of the order 10-8 A°. It refers to the extent of both oxidation and reduction that occurs.
is known as exchange current density. It may be defined, as "the flow of charge or electrons across an electrochemical system in equilibrium". Its value normally is very low, of the order 10-8 A°. It refers to the extent of both oxidation and reduction that occurs.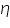 )
) 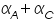 ).
).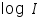 values are plotted against over potential we get Tafel plots. These offer simple method for experimentally determining
values are plotted against over potential we get Tafel plots. These offer simple method for experimentally determining 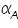 and from cathodic slope
and from cathodic slope 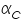 can be determined. This value is very important in industrial practice. This determines the potential that is to be applied to affect the desired rate of reduction or oxidation.
can be determined. This value is very important in industrial practice. This determines the potential that is to be applied to affect the desired rate of reduction or oxidation.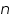 ' for an unknown reaction can be determined. This reflects on the mechanism of the reaction; that is how many electrons are involved in that step. Whether the reaction is single step or multi step is revealed by this value.
' for an unknown reaction can be determined. This reflects on the mechanism of the reaction; that is how many electrons are involved in that step. Whether the reaction is single step or multi step is revealed by this value.