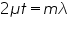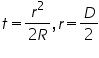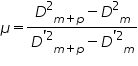| . | . | |||
| . | Newton's Rings-Refractive index of liquid |
. | ||
| . |
Aim:
Thin film interference:
A film is said to be thin when its thickness is about the order of one wavelength of visible light which is taken to be 550 nm. When light is incident on such a film, a small portion gets reflected from the upper surface and a major portion is transmitted into the film. Again a small part of the transmitted component is reflected back into the film by the lower surface and the rest of it emerges out of the film. These reflected beams reunite to produce interference. Also the transmitted beams too interfere. This type of interference that takes place in thin films is called interference by division of amplitude.
Θ1 angle of incidence at medium 1 to medium 2 boundary.
In the above figure the rays r12 and t21 interfere and results in a constructive or destructive interference depending on their path differences, given as,
Where,
To find the refractive index of liquid:
The experiment is performed when there is an air film between the plano-convex lens and the optically plane glass plate.The diametre of the mth and the (m+p)th dark rings are determined with the help of a travelling microscope.
For air
As shown in figure arrange the lens with glass plate. Pour one or two drops of liquid whose refractive index is to be determined without disturbing the arrangement. Now the air film between the lens and glass plate is replaced by the liquid. The diameters of m+pth and mth rings are determined.
For liquids,
For normal incidence cosr =1,so But Rearranging the above equation ,we get
We have for liquids,
From these two euations the refractive index of the given liquids is given by
Cite this Simulator: |
..... | ||
| ..... | ..... | |||
 |
Copyright @ 2024 Under the NME ICT initiative of MHRD |
 |



 destructive interference
destructive interference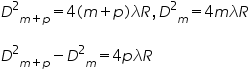
.jpg)
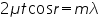 ,for dark rings
,for dark rings