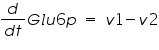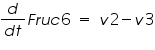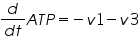Objective:

 

• To learn how to develop and simulate a mathematical model using Cell Designer

 

Introduction:

 

Cell contains the genetic material DNA, which encodes for proteins.These proteins perform many important functions, some of which include acting as enzymes, providing energy for metabolic activities, giving shape to cell and enable motility to the cell. Proteins play an important role in cell signaling. Modeling, reverse engineering and analysis of these macromolecular complex networks have interested the computational biologists, which lead them to develop specific tools like cytoscape, cell designer, E-cell, J-Designer etc. All these tools take input as existing network which is curated and stored in databases like KEGG, BIOCARTA, Interactome and some organism specific databases.

 

Systems biology deals with mainly modeling of biological systems at a system level. The main purpose of CellDesigner is to draw networks using symbolic notation which is proposed by Kitano. CellDesigner helps to create and simulate a model mathematically. Simulate the reaction by changing conditions of TIME Vs Substance. Simulation of the reaction can be done by changing the different conditions and the results can be viewed graphically with time on the X-axis and species(or substances) on the Y-axis. It implies that, at a particular time what will be expression of particular substance, based on an equation.

 

Features of cell designer:

 

• The user can draw reaction easily

 

• The user can open a model from a pre-existing repository

 

• Data can be read and written in SBML format

 

• Simulate reactions by changing the conditions and can view results graphically

 

What is a model :

 

A model is a representation of any object or a system. It is important to highlight that a model is not the real object/system, but only a human construct to help us to understand real object/systems. In general all models have an input, a processor, and an output of expected results. In mathematical modelling, one can translate the values into the language of mathematics.

 

 

What is a mathematical model :

 

Mathematical equations must be chosen to describe the system, when the structure of a model has been determined. We have to carefully choose formulations since they can have unexpected effects on the behavior of the model. The modeling part mainly depends on formulation, analysis, interpretation and testing of the model.

 

Process of mathematical modelling:

 

 

 

Figure 1: Process of mathematical modelling.

 

 Principles of Mathematical modelling:

 

• To identify the need for the model.

 

• Find the required data.

 

• Assume the conditions that has to be applied to the data.

 

• Identify the governing physical principles.

 

• Predict the equations and calculations, and the output that would result.

 

• Valid tests can be made to validate the model, and check whether, it is reliable with its principles and assumptions.
   

 

Mathematical modelling and simulation in CellDesigner :

 

Systems biology is concerned with modelling of biological systems at a systems level. Consider the interactions of all the components of a system rather than its isolated properties. Biological systems such as cells, regulatory gene networks and protein interaction complexes cannot be understood from individual components like proteins, genes and mRNA. It must be understood through the networks involving all components at the same time. It is mainly focusing on the stochastic modelling and computer simulation techniques for analyzing the systems.

 

A simple mathematical model for enzyme substrate reaction comprises of a reversible formation of an enzyme-substrate complex ES. This complex is formed from the available free enzyme 'E', substrate 'S' and an irreversible release of product 'P' from the enzyme 'E'. The respective system of ODEs for the dynamics of this reaction is read as follows.

 

 

 Figure 2: Enzyme substrate reaction.

 

The metabolic network consists of reactions where one type of molecule is transformed to another type. A simple mathematical equation for a metabolic network is as follows.

 

 

 Figure 3: Sample network 

 

The ODE system for this reaction system is given by:

 

[v = k * conc.of the reactants]

 

Where:   v= Rate of reaction;  k= Rate constant.
 

Calculation: 

 

NOTE: The rate of change of Glucose-6-phosphate is the rate of formation of Glucose-6-phosphate (v1) and the rate of degradation of Glucose-6-phosphate (-v2).

 

 Here : -v represents degradation.

 

Rate of change of Glucose-6-phosphate = rate of formation of Glucose-6-phosphate (v1)- rate of degradation of Glucose-6-phosphate (-v2,-v3)
 

 

 

 

Cell Designer GUI is divided into several frames.

 

 

Figure 5: GUI of CellDesigner

 

Drawing features of CellDesigner

 

 

 

 Figure 6: Drawing featurs of CellDesigner