
| . | . | |||
| . | Harvesting a Prey Population |
. | ||
| . |
Objectives
1) To understand the concept of harvesting.
2) To study this concept with the help of mathematically defined equations.
In a predator-prey system, the prey is consumed by the predator to survive while the prey continuously adds individuals to the system as they are hunted down to maintain the state of equilibrium. On the other hand, human interaction with nature is quite the contrary. Primitive human beings used to hunt down animals or harvest the crops yield, leaving behind a group of individuals to grow for future harvest. The concept of harvesting comes only when the interaction involves human beings as we kill or harvest a proportion of individuals unlike a typical predator. The day-to-day human activities like agriculture, rearing cattle, sheep, hens etc. come under the category of harvesting. Human beings learnt how to do agriculture and they harvest the product at the time of ripening. During evolution, we learnt how to make use of these things and harvest them for beneficial purpose. Many typical examples support the harvesting phenomena like growing cattle’s and sheep for their milk and wool, maintaining poultry farms for their meat, maintaining fisheries for fish, etc. Fisheries are another important area where the harvesting is done with extreme caution. In order to maintain an equilibrium state the proportion of individuals that are harvested depends on the maximum sustainable yield (MSY). MSY refers to the maximum number of individuals that can be harvested from the population which equals the recruitment rate of that population. Recruitment rate refers to the number of new individuals added to the existing population. High yields are obtained from populations held below, often well below, the carrying capacity. Recruitment rate is low when there are few individuals and low when there is intense intraspecific competition. It is zero at the carrying capacity (K). MSY targets to sustain the population size at the point of maximum rate of growth by harvesting the individuals that would normally be added to the population, allowing population to be productive indefinitely. While highlighting the advantages of using MSY concept, we should also be aware of some of the drawbacks according to Larkin, 1977. These include:
1) It put populations at too much risk.
2) It did not account for spatial variability in productivity.
3) It did not account for species other than the focus of the fishery.
4) It considered only the benefits, not the costs, of fishing.
5) It was sensitive to political pressure.
In this interaction, the predator dynamics is not considered as they are not involved. As the predator dynamics is not involved, in the classical logistic equations for predator and prey used in the earlier simulators we neglect the terms related to predator dynamics. As the additional component “Harvesting” is considered in the prey dynamics we add a term related to the harvesting component. As previously mentioned in this exercise we consider harvesting at a rate less than the MSY in order to ensure the risk free environment. In the below equation, we add the term “h” which refers to the harvesting rate to the prey dynamics. In the equation included with harvesting rate does not consider the spatial distribution of the individuals (theta) or it is assigned a value of 1. We consider the spatial distribution of the individuals under the effect of theta value on MSY.
Our classical logistic equation in the earlier simulators for the prey looks like
Now an extra term “h” is added to the equation above mentioned.
In the above equation we consider the theta (θ) value to be 1 for harvesting at less than maximum sustainable yield.
rm refers to the rate of growth of the species,
N refers to the species population,
K refers to the carrying capacity,
h is the rate of harvesting.
Using the above mentioned equation, we try with two different initial densities. And later we try to find out what happens if we add 25 individuals to the population and we remove 25 individuals from the population with the help of the mathematical simulator given in this exercise. Depending on the initial population densities the graph is plotted respectively.
Now, we reuse the prey equation above with harvesting rate with the theta value assigned by the user. The modified equation looks like
Θ refers to the spatial distribution of the individuals.
rm refers to the rate of growth of the species,
N refers to the species population,
K refers to the carrying capacity,
h is the rate of harvesting.
The user can try out with different theta values to see the effect on the MSY.
Note:
Please check "Procedure tab" if you have issues loading the simulator.
Cite this Simulator: |
..... | ||
| ..... | ..... | |||
 |
Copyright @ 2024 Under the NME ICT initiative of MHRD |
 |

![Double click to edit «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac»«mrow»«mi»d«/mi»«mi»N«/mi»«/mrow»«mrow»«mi»d«/mi»«mi»t«/mi»«/mrow»«/mfrac»«mo»=«/mo»«msub»«mi»r«/mi»«mi»m«/mi»«/msub»«mo»*«/mo»«mi»N«/mi»«mo»*«/mo»«mfenced close=¨]¨ open=¨[¨»«mrow»«mn»1«/mn»«mo»-«/mo»«mo»(«/mo»«mfrac»«mi»N«/mi»«mi»K«/mi»«/mfrac»«msup»«mo»)«/mo»«mi»§#952;«/mi»«/msup»«/mrow»«/mfenced»«/math»](/fckeditor/editor/plugins/fckeditor_wiris/integration/showimage.php?formula=e36b651589c20cea364f7b6aa24ad500.png)
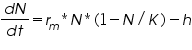
![Double click to edit «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac»«mrow»«mi»d«/mi»«mi»N«/mi»«/mrow»«mrow»«mi»d«/mi»«mi»t«/mi»«/mrow»«/mfrac»«mo»=«/mo»«msub»«mi»r«/mi»«mi»m«/mi»«/msub»«mo»*«/mo»«mi»N«/mi»«mo»*«/mo»«mfenced close=¨]¨ open=¨[¨»«mrow»«mn»1«/mn»«mo»-«/mo»«mo»(«/mo»«mfrac»«mi»N«/mi»«mi»K«/mi»«/mfrac»«msup»«mo»)«/mo»«mi»§#952;«/mi»«/msup»«/mrow»«/mfenced»«mo»-«/mo»«mi»h«/mi»«/math»](/fckeditor/editor/plugins/fckeditor_wiris/integration/showimage.php?formula=0a91abed4ab1f0cce27fbd4958b2bd3c.png)