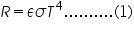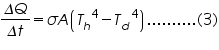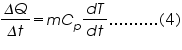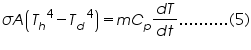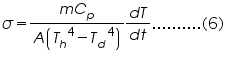| . | . | |||
| . | Black Body Radiation: Determination of Stefan's Constant |
. | ||
| . | Aim:
Determination of Stefan- Boltzmann constant ÃÂÆ’ .
Apparatus:
Heater, temperature-indicators, box containing metallic hemisphere with provision for water-flow through its annulus, a suitable black body which can be connected at the bottom of this metallic hemisphere.
Principle:
A black body is an ideal body which absorbs or emits all types of electromagnetic radiation. The term ‘black body’ was first coined by the German physicist Kirchhoff during 1860’s. Black body radiation is the type of electromagnetic radiation emitted by a black body at constant temperature. The spectrum of this radiation is specific and its intensity depends only on the temperature of the black body. It was the study of this phenomenon which led to a new branch of physics called Quantum mechanics.
Where R = energy radiated per area per time, Ä = emissivity of the material of the body, ÃÂÆ’ = Stefan’s constant = 5.67x10-8 Wm-2K-4, and T is the temperature in Kelvin scale.
Josef Stefan Ludwig Boltzmann
For an ideal black body, emissivity Ä=1, and equation (1) becomes,
The block diagram of experimental set up to study the blackbody radiation is given below.
figure(1)
This setup uses a copper disc as an approximation to the black body disc which absorbs radiation from the metallic hemisphere as shown in fig (1). Let Td and Th is the steady state temperatures of copper disc and metallic hemisphere respectively. Now according to the equation (2), the net heat transfer to the copper disc per second is,
Where A is the area of the copper disc and ÃŽâ€ÂQ= (Qh-Qd).
Now, we have another equation from thermodynamics for heat transfer as,
Where ‘m’ mass of the disc, ‘Cp’’ specific heat of the copper, dT/dt is the change in temperature per unit time.
Equating equations (3) and (4),
Hence,
Applications:
Cite this Simulator: |
..... | ||
| ..... | ..... | |||
 |
Copyright @ 2024 Under the NME ICT initiative of MHRD |
 |