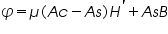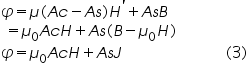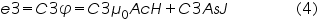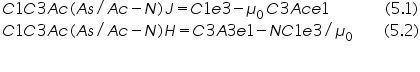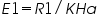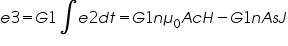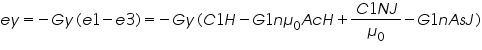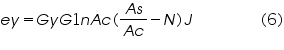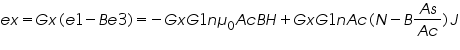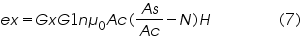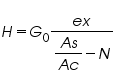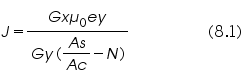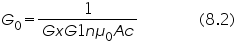| . | . | |||
| . | Magnetic Material Characterization via Hystersis (Remote Trigger) |
. | ||
| . |
Theory
Hysteresis
Hysteresis means “remaining†in Greek, an effect remains after its cause has disappeared. Hysteresis, a term coined by Sir James Alfred Ewing in 1881, a Scottish physicist and engineer (1855-1935), defined it as: "When there are two physical quantities M and N such that cyclic variations of N cause cyclic variations of M, then if the changes of M lag behind those of N, we may say that there is hysteresis in the relation of M to N". The most notable example of hysteresis in physics is magnetism. Iron maintains some magnetization after it has been exposed to and removed from a magnetic field.
Magnetic Hysteresis
Consider a magnetic material being subjected to a cycle of magnetization.The graph intensity of magnetization (M) vs. magnetizing field (H) gives a closed curve called M-H loop.Consider the portion AB of the curve given below.The intensity of magnetization M does not become zero when the magnetizing field H is reduced to zero.Thus the intensity of magnetization M at every stage lags behind the applied field H.This property is called magnetic hysteresis.The M-H loop is called hysteresis loop.The shape and area of the loop are different for different materials.
Hysteresis Loop
An initially unmagnetized material is subjected to a cycle of magnetization.The values of intensity of magnetization M and the magnetizing field H are calculated at every stage and a closed loop is obtained on plotting a graph between M and H as shown in the figure.The point ‘O’ represents the initial unmagnetized condition of the material.As the applied field is increased, the magnetization increases to the saturation point ‘A’ along ‘OA’.As the applied field is reduced, the loop follows the path ‘AB’.‘OB’ represents the intensity of magnetization remaining in the material when the applied field is reduced to zero.This is called the residual magnetism or remanence.The property of retaining some magnetism on removing the magnetic field is called retentivity.OC represents the magnetizing field to be applied in the opposite direction to remove residual magnetism.This is called coercive field and the property is called coercivity.When the field is further increased in the reverse direction the material reaches negative saturation point ‘D’.When the field is increased in positive direction, the curve follows path ‘DEF’.
Hysteresis Loop Tracer Design Principle
When a cylindrical sample is placed coaxially in a periodically varying magnetic field produced by the solenoid, the magnetisation in the sample undergoes a periodic variation. The pickup coil placed coaxially with the sample picks up this variation. For the uniform field Ha produced by the solenoid, the effective field H acting on the cylindrical sample will be,
Where M is magnetization, or H = Ha – NJ/μo , where N is the normalized demagnetization factor and J is the magnetic polarization defined by, B = μoH + J with B = μH = μo(H+M) as magnetic induction. The signal corresponding to the applied field, Ha, can be written as,
Further the flux linked with the pick-up coil of area Ac due to the sample of area As will be
Here H’ is the magnetic field, in the free from sample area of the pickup coil, will be different from H and the difference will be determined by the magnitude of the demagnetizing field. However, when the ratio of the length of the sample rod to the diameter of the pickup coil is more than 10, the difference between H and H’ is too small, so we have
The signal e2 induced in the pickup coil will be proportional to dÆ/dt. After the integration the signal (e3) will therefore be
Solving (1),(2) and (4) for J and H gives:
In case the sample contains a number of magnetically different constituents, the loop obtained is the algebraic sum of individual loops of different phases.The separation of these is not easy in a J-h loop, while in a second derivative of J with respect to time, d2j/dt2, the identification can be made very clear.Now the aim is to produce electrical signals corresponding to J and H as defined above by equations (5.1) and (5.2) so that they can be displayed on the CRO (Cathode Ray Oscilloscope).Moreover, it s to display dÆ/dt and d2Æ/dt2 as a function of H.
The magnetic field is obtained with a multilayered solenoid driven by the AC mains at 50Hz and by a variable transformer arrangement.The instantaneous current producing the field is passed through a resistor R1 in series with the solenoid.The signal e2 corresponding to the rate of change of flux is obtained from a pickup coil wound on a non conducting tube.Necessary arrangements have been made to place the sample coaxially with the pickup winding and in uniform magnetic field.
The signals e1 and e3 are added and its output which is proportional to J is applied to Y-input of CRO.Fractions of these signals corresponding to the demagnetization factor and area ratio are added, amplified and the output is fed to the X-input input of CRO which gives H.The selector switch can change the Y-input of CRO to J, dj/dt , or d2j/dt2. The dj/dt signal is directly taken from the pick-up coil while d2j/dt2 is obtained through the differentiator.
Now the magnetic field at the centre of the solenoid for current I flowing through it will be, Ha = Ki or e1 = R1i
Substituting Æfrom Equation (3) above we get, e2 = nμ0Ac(dH/dt)+nAs(dJ/dt) Now as mentioned earlier integrating e2 gives e3. So,
Where G1 is the gain of the integrator and phase shifter combination. Again as mentioned above out of phase signals e1 and –e3 are added and after suitable amplification Gy, becomes,
If we adjust C1 = H , then
Fraction α and β of e1 and –e3 respectively, are added together and amplified (let us say by the factor Gx) for the X-input. So we get,
After substituting C1 =g1nµ0 Ac, J is eliminated from the right hand side and by adjusting α and β such that
We get,
Equations (6) and (7) can be written as:
Where,
Equations (8.1) and (8.2) define the physical quantities H and J in terms of electrical signals ex and ey respectively.
Cite this Simulator: |
..... | ||
| ..... | ..... | |||
 |
Copyright @ 2025 Under the NME ICT initiative of MHRD |
 |


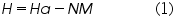
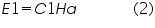 ,where C1 is a constant
,where C1 is a constant