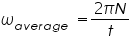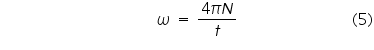| . | . | |||
| . | Moment of Inertia of Flywheel |
. | ||
| . | Aim:
To determine the moment of inertia of a flywheel. Apparatus:
Fly wheel, weight hanger, slotted weights, stop watch, metre scale. Theory: The flywheel consists of a heavy circular disc/massive wheel fitted with a strong axle projecting on either side.The axle is mounted on ball bearings on two fixed supports. There is a small peg on the axle. One end of a cord is loosely looped around the peg and its other end carries the weight-hanger.
Let "m" be the mass of the weight hanger and hanging rings (weight assembly).When the mass "m" descends through a height "h", the loss in potential energy is
The resulting gain of kinetic energy in the rotating flywheel assembly (flywheel and axle) is
Where I -moment of inertia of the flywheel assembly ω-angular velocity at the instant the weight assembly touches the ground.
The gain of kinetic energy in the descending weight assembly is,
Where v is the velocity at the instant the weight assembly touches the ground.
The work done in overcoming the friction of the bearings supporting the flywheel assembly is
Where n - number of times the cord is wrapped around the axle Wf - work done to overcome the frictional torque in rotating the flywheel assembly completely once Therefore from the law of conservation of energy we get
Now the kinetic energy of the flywheel assembly is expended in rotating N times against the same frictional torque. Therefore If r is the radius of the axle, then velocity v of the weight assembly is related to r by the equation
Substituting the values of v and Wf we get:
Now solving the above equation for I
Where, I = Moment of inertia of the flywheel assembly N = Number of rotation of the flywheel before it stopped m = mass of the rings n = Number of windings of the string on the axle g = Acceleration due to gravity of the environment. h = Height of the weight assembly from the ground. r = Radius of the axle.
Now we begin to count the number of rotations, N until the flywheel stops and also note the duration of time t for N rotation. Therefore we can calculate the average angular velocity Since we are assuming that the torsional friction Wf is constant over time and angular velocity is simply twice the average angular velocity
Applications:
Flywheels can be used to store energy and used to produce very high electric power pulses for experiments, where drawing the power from the public electric network would produce unacceptable spikes. A small motor can accelerate the flywheel between the pulses.
Cite this Simulator: |
..... | ||
| ..... | ..... | |||
 |
Copyright @ 2024 Under the NME ICT initiative of MHRD |
 |


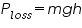
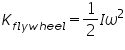
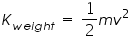
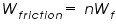
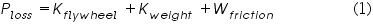
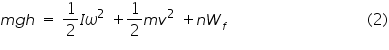
 and
and 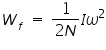
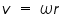
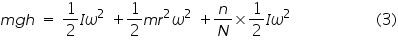

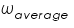 in radians per second.
in radians per second.