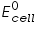| . | . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| . | EMF measurement |
. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| . |
Objectives:
Theory:
Electrode at which oxidation takes place is anode and the electrode at which reduction takes place is cathode. When a metal is in contact with its own ion solution it develops a potential with respect to the electrolyte. The potential difference developed at the anode - electrolyte interface is called oxidation potential and the potential difference developed at the cathode -electrolyte interface is called reduction potential. The potential difference between the anode and cathode is called the EMF of the cell. The potential difference measured at standard conditions (1 atm pressure, 273K) is called standard electrode potential. Standard electrode potential gives the tendency of the electrode to get oxidized or reduced. If the electrolytes are different the two compartments are joined by a salt bridge, which is a tube containing a concentrated electrolyte solution in agar jelly that completes the electrical circuit and enables the cell to function.
Electrochemical Series:
A series in which metals are arranged in the decreasing order of reduction potential.
We can construct innumerable number of galvanic cells by taking combinations of different half cells. Each half cell consists of a metallic road dipped in to an electrolyte. The metal with higher reduction potential act as cathode and the other will act as anode.
Standard EMF of the cell:
A galvanic cell is represented by putting a vertical line between metal and electrolyte solution and putting a double vertical line between the two electrolytes connected by a salt bridge.
Eg: The symbolic representation of Daniel cell is given below,
First, the reduced form of the metal to be oxidized at the anode (Zn) is written. This is separated from its oxidized form by a vertical line, which represents the limit between the phases (oxidation changes). The double vertical lines represent the saline bridge on the cell. Finally, the oxidized form of the metal to be reduced at the cathode, is written, separated from its reduced form by the vertical line. The electrolyte concentration is given as it is an important variable in determining the cell potential.
Standard Hydrogen Electrode (S.H.E.):
The potential of Standard hydrogen electrode used as the reference electrode has been arbitrarily taken as zero. The electrode consist of a glass jacket consisting of dry hydrogen gas bubbled at one atmosphere. There is a platinum wire sealed in the glass jacket. The entire system is immersed in 1M HCl solution. Standard hydrogen electrode can be represented as,
Electrode potential at any concentration can be calculated using Nernst equation. For the reaction,
Nernst Equation,
Where;
When a cell reaction takes place electrical energy is produced which results in decrease in the free energy of the system.
Electrical work = Decrease in free energy In an electro chemical cell, Electric work done = Quantity of electric charge produced x E.M.F of the cell
For one mole of electrons quantity of electric charge is 1
Therefore, for
For a standard cell,
By van 't Hoff relation,
Spontaneity or Feasibility of Reaction:
Cite this Simulator: |
..... | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ..... | ..... | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
Copyright @ 2024 Under the NME ICT initiative of MHRD |
 |

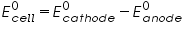
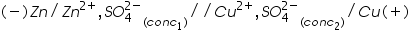
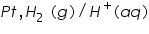
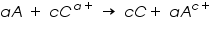
![Double click to edit «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi»E«/mi»«mrow»«mi»c«/mi»«mi»e«/mi»«mi»l«/mi»«mi»l«/mi»«/mrow»«/msub»«mo»=«/mo»«msubsup»«mi»E«/mi»«mrow»«mi»c«/mi»«mi»e«/mi»«mi»l«/mi»«mi»l«/mi»«/mrow»«mn»0«/mn»«/msubsup»«mfrac»«mrow»«mn»2«/mn»«mo».«/mo»«mn»303«/mn»«mi»R«/mi»«mi»T«/mi»«/mrow»«mrow»«mi»n«/mi»«mi»F«/mi»«/mrow»«/mfrac»«mo»-«/mo»«mfrac»«mrow»«mi mathvariant=¨normal¨»log«/mi»«mo»[«/mo»«msup»«mi»C«/mi»«mrow»«mi»a«/mi»«mo»+«/mo»«/mrow»«/msup»«msup»«mo»]«/mo»«mi»c«/mi»«/msup»«/mrow»«msup»«mfenced close=¨]¨ open=¨[¨»«msup»«mi»A«/mi»«mrow»«mi»c«/mi»«mo»+«/mo»«/mrow»«/msup»«/mfenced»«mi»a«/mi»«/msup»«/mfrac»«/math»](/fckeditor/editor/plugins/fckeditor_wiris/integration/showimage.php?formula=5261c921c1b1d415e94d309dcaa630c5.png)

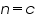 if
if 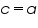
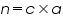 if
if 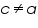
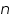 = number of electrons.
= number of electrons.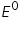 = electrode potential of cell at standard conditions.
= electrode potential of cell at standard conditions.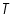 = temperature.
= temperature.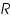 = universal gas constant.
= universal gas constant.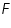 = Faraday constant.
= Faraday constant.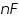 .
.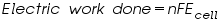
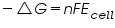
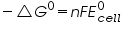
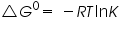
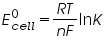
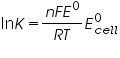
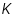 = equilibrium constant
= equilibrium constant