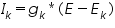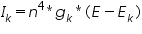| . | . | |||
| . | Modeling the delayed rectifier Potassium channels |
. | ||
| . |
Objective
1) Understanding the importance of K+ channels and how it serves as a delayed rectifier.
Ionic channels are very important in shaping the signals carried which is regulated by their opening and closing mechanisms and working concertly with other ionic channels. The membrane has different ionic channels specified for specific ions. Along with these ionic channels, ionic pumps exist which were ATP-dependent. Like voltage-gated sodium channel, potassium ions also use their specific voltage-gated potassium channel except that they don’t have time-sensitive gate like in voltage-gated sodium channel. Potassium channels were known to play a major role in the repolarization phase of the action potential. It so happens that the membrane at the rest seems to passively diffuse potassium ions. Membrane is selectively permeable to K+ ions even at the rest state. Movement of the potassium ions creates a concentration gradient as can be observed from the Figure 1. One of the main reasons that inside of the cell is negative and outside positive, because due to the metabolism, the cell produces acids which release protons away and keep the organic anions. During the depolarization, the positive atmosphere is increased inside leading to the increase in the membrane potential.
Gating phenomenon is common in these ionic channels. It keeps open the ionic channel open for few milliseconds and then for each second, it was known that about 107 ions were allowed to pass through the channel. All the membrane biophysics obeys simple electrical laws like ohm’s law, Kirchhoff’s law, etc. Ohm's law plays a central role in membrane biophysics because each ionic channel is an elementary conductor spanning the insulating lipid membrane. The total conductance of a membrane is the sum of all these elementary conductances in parallel. It is a measure of how many ionic channels are open, how many ions are available to go through them, and how easily the ions pass. It is a simple relationship between current, voltage and conductance.
Membrane acts like a capacitor and the channel acts like a conductor. Ohm's law cannot be applied directly but with a change in the equation, it can be used. Some of the biophysical laws like Nernst Equation, GHK equation were used to calculate the equilibrium potentials according to their concentration gradients inside and outside.
The above equation shows Nernst equation for calculating the equilibrium potential for each ion separately. Unfortunately, Nernst equation could not be used more accurately as it considers single ionic species. As mentioned earlier, membrane has several ionic channels so we use GHK equation.
And the ohm’s law as explained above cannot be used for testing on membrane. A small modification in the equation should be done as shown below.
The size of the needed ionic flux depends on the surface area of the cell, whereas the effect of the flux on internal ionic concentrations depends on the volume of the cell. The ionic channel mechanisms were affected by the gating particles. The gating particles contribute significantly to the gating mechanism. According to Hodgkin and Huxley, in their model they considered there were particles called “n” regulated the potassium channel gating mechanism. So, in the equation describing the potassium current calculation, they added the term n4 to the equation, so it looks like this after modification.
Voltage-sensitive ionic permeabilities are found in virtually all eukaryotic cells. These voltage-gated K channels have a very large diversification. Most open only after the membrane is depolarized, but some only after it is hyperpolarized. Some open rapidly and some, slowly. Some are strongly modulated by neurotransmitters or intracellular messengers. K+ ion s are always the major current carrier, the responses and the pharmacology differ enough to require that fundamentally different channels are involved. Each excitable membrane uses a different mix of these several K channels to fulfill its need. The K channel of axons was given the name "delayed rectifier" because it changes the membrane conductance with a delay after a voltage step. This name is still used to denote axon-like K channels, even though almost all of the other known kinds of K channels also change membrane conductance with a delay. With them, cells can regulate pace make potentials, generate spontaneous trains and bursts of action potentials, make long plateaus on action potentials, or regulate the overall excitability of the cell.
Open K channels stabilize the membrane potential. They draw the membrane potential closer to the potassium equilibrium potential and farther from the firing threshold. In excitable cells, the roles of all types of K channels are related to this stabilization. Potassium channels set the resting potential, keep fast action potentials short, terminate periods of intense activity, time of the inter-spike intervals during repetitive firing, and generally lower the effectiveness of the excitatory inputs on a cell when they are open.
Note:
|
..... | ||
| ..... | ..... | |||
 |
Copyright @ 2025 Under the NME ICT initiative of MHRD |
 |

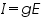
![Double click to edit «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi»E«/mi»«mrow»«mi»r«/mi»«mi»e«/mi»«mi»v«/mi»«/mrow»«/msub»«mo»=«/mo»«mfenced»«mrow»«mi»R«/mi»«mi»T«/mi»«mo»/«/mo»«mi»z«/mi»«mi»F«/mi»«/mrow»«/mfenced»«mo»*«/mo»«mi mathvariant=¨normal¨»ln«/mi»«mo»*«/mo»«mfenced close=¨]¨ open=¨[¨»«mrow»«mi»I«/mi»«mi»o«/mi»«mi»n«/mi»«mo»§nbsp;«/mo»«mi»c«/mi»«mi»o«/mi»«mi»n«/mi»«mi»c«/mi»«mo».«/mo»«mo»§nbsp;«/mo»«mi»i«/mi»«mi»n«/mi»«/mrow»«/mfenced»«mo»/«/mo»«mfenced close=¨]¨ open=¨[¨»«mrow»«mi»I«/mi»«mi»o«/mi»«mi»n«/mi»«mo»§nbsp;«/mo»«mi»c«/mi»«mi»o«/mi»«mi»n«/mi»«mi»c«/mi»«mo».«/mo»«mo»§nbsp;«/mo»«mi»o«/mi»«mi»u«/mi»«mi»t«/mi»«/mrow»«/mfenced»«/math»](/fckeditor/editor/plugins/fckeditor_wiris/integration/showimage.php?formula=fd498bb1b8eee7f1125501c9d0ce042e.png)
![Double click to edit «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi»V«/mi»«mi»m«/mi»«/msub»«mo»=«/mo»«mfrac»«mrow»«mi»R«/mi»«mi»T«/mi»«/mrow»«mi»F«/mi»«/mfrac»«mo»*«/mo»«mi mathvariant=¨normal¨»ln«/mi»«mo»*«/mo»«mfenced»«mrow»«msub»«mi»P«/mi»«mi»k«/mi»«/msub»«msub»«mfenced close=¨]¨ open=¨[¨»«msup»«mi»K«/mi»«mo»+«/mo»«/msup»«/mfenced»«mi»o«/mi»«/msub»«mo»+«/mo»«msub»«mi»P«/mi»«mrow»«mi»N«/mi»«mi»a«/mi»«/mrow»«/msub»«msub»«mfenced close=¨]¨ open=¨[¨»«mrow»«mi»N«/mi»«msup»«mi»a«/mi»«mo»+«/mo»«/msup»«/mrow»«/mfenced»«mi»o«/mi»«/msub»«mo»+«/mo»«msub»«mi»P«/mi»«mrow»«mi»C«/mi»«mi»l«/mi»«/mrow»«/msub»«msub»«mfenced close=¨]¨ open=¨[¨»«mrow»«mi»C«/mi»«msup»«mi»l«/mi»«mo»-«/mo»«/msup»«/mrow»«/mfenced»«mi»i«/mi»«/msub»«mo»/«/mo»«msub»«mi»P«/mi»«mi»k«/mi»«/msub»«msub»«mfenced close=¨]¨ open=¨[¨»«msup»«mi»K«/mi»«mo»+«/mo»«/msup»«/mfenced»«mi»i«/mi»«/msub»«mo»+«/mo»«msub»«mi»P«/mi»«mrow»«mi»N«/mi»«mi»a«/mi»«/mrow»«/msub»«msub»«mfenced close=¨]¨ open=¨[¨»«mrow»«mi»N«/mi»«msup»«mi»a«/mi»«mo»+«/mo»«/msup»«/mrow»«/mfenced»«mi»i«/mi»«/msub»«mo»+«/mo»«msub»«mi»P«/mi»«mrow»«mi»C«/mi»«mi»l«/mi»«/mrow»«/msub»«msub»«mfenced close=¨]¨ open=¨[¨»«mrow»«mi»C«/mi»«msup»«mi»l«/mi»«mo»-«/mo»«/msup»«/mrow»«/mfenced»«mi»o«/mi»«/msub»«mo»§nbsp;«/mo»«/mrow»«/mfenced»«mo»§nbsp;«/mo»«/math»](/fckeditor/editor/plugins/fckeditor_wiris/integration/showimage.php?formula=3878253139c27273cff67804e3073fa9.png)