
| . | . | |||
| . | Global alignment of two sequences - Needleman-Wunsch Algorithm |
. | ||
| . |
Objective
Theory
The most commonly asked question in molecular biology is whether two given sequences are related or not, in order to identify their structure or function. The most simpler way to answer this question is to compare their sequences.
Sequence is a collection of nucleotides or amino acid residues which are connected with each other. Speaking biologically, a typical DNA/RNA sequence consist of nucleotides while a protein sequence consist of amino acids.
Sequencing is the process to determine the nucleotide or amino acid sequence of a DNA fragment or a protein. There are different experimental methods for sequencing, and the obtained sequence is submitted to different databases like NCBI, Genbank etc.
Methods of Sequencing:
Sequences stored in the database were obtained from different experimental methods. Most commonly used methods for DNA sequencing are Sanger Method and Maxam-Gilbert Method. Similarly Edman Degradation method and Mass Spectrometry technique are used for protein sequencing.
Sanger Method (dideoxy chain termination method): Here 4 test tubes are taken labelled with A, T, G and C. Into each of the test tubes, DNA has to be added in denatured form (single strands). Next a primer is to be added which anneals to one of the strand in template. The 3' end of the primer accomodates the dideoxy nucleotides [ddNTPs] (specific to each tube) as well as deoxy nucleotides randomly. When the ddNTP's gets attached to the growing chain, the chain terminates due to lack of 3'OH which forms the phospho diester bond with the next nucleotide. Thus small strands of DNA are formed. Electrophoresis is done and the sequence order can be obtained by analysing the bands in the gel based on the molecular weight. The primer or one of the nucleotides can be radioactively or fluorescently labeled also, so that the final product can be detected from the gel easily and the sequence can be inferred.
Maxam-Gilbert (Chemical degradation method): This method requires denatured DNA fragment whose 5' end is radioactively labeled. This fragment is then subjected to purification before proceeding for chemical treatment which results in a series of labeled fragments. Electrophoresis technique helps in arranging the fragments based on their molecular weight. To view the fragments, gel is exposed to X-ray film for autoradiography. A series of dark bands will appear, each corresponding to a radio labeled DNA fragment, from which the sequence can be inferred.
Edman Degradation reaction: The reaction finds the order of amino acids in a protein by cleaving each amino acid from the N-terminal without distrubing the bonds in the protein. After each clevage, chromatography or electrophoresis is done to identify the amino acid.
Mass Spectrometry: It is used to determine the mass of particle, composition of molecule and for finding the chemical structures of molecules like peptides and other chemical compounds. Based on the mass to charge ratio, one can identify the amino acids in a protein.
Sequence Alignment and importance:
Sequence Alignment or sequence comparison lies at heart of the bioinformatics, which describes the way of arrangement of DNA/RNA or protein sequences, in order to identify the regions of similarity among them. It is used to infer structural, functional and evolutionary relationship between the sequences. Alignment finds similarity level between query sequence and different database sequences. The algorithm works by dynamic programming approach which divides the problem into smaller independent sub problems. It finds the alignment more quantitatively by assigning scores.
When a new sequence is found, the structure and function can be easily predicted by doing sequence alignment. Since it is believed that, a sequence sharing common ancestor would exhibit similar structure or function. Greater the sequence similarity, greater is the chance that they share similar structure or function.
Methods of Sequence Alignment:
There are mainly two methods of Sequence Alignment:
Global Alignment : Closely related sequences which are of same length are very much appropriate for global alignment. Here, the alignment is carried out from beginning till end of the sequence to find out the best possible alignment.
The Needleman-Wunsch algorithm (A formula or set of steps to solve a problem) was developed by Saul B. Needleman and Christian D. Wunsch in 1970, which is a dynamic programming algorithm for sequence alignment. The dynamic programming solves the original problem by dividing the problem into smaller independent sub problems. These techniques are used in many different aspects of computer science. The algorithm explains global sequence alignment for aligning nucleotide or protein sequences.
Local Alignment : Sequences which are suspected to have similarity or even dissimilar sequences can be compared with local alignment method. It finds local regions with high level of similarity.
These two methods of alignments are defined by different algorithms, which use scoring matrices to align the two different series of characters or patterns (sequences). The two different alignment methods are mostly defined by Dynamic programming approach for aligning two different sequences.
Dynamic Programming:
Dynamic programming is used for optimal alignment of two sequences. It finds the alignment in a more quantitative way by giving some scores for matches and mismatches (Scoring matrices), rather than only applying dots. By searching the highest scores in the matrix, alignment can be accurately obtained. The Dynamic Programming solves the original problem by dividing the problem into smaller independent sub problems. These techniques are used in many different aspects of computer science. Needleman-Wunsch and Smith-Waterman algorithms for sequence alignment are defined by dynamic programming approach.
Scoring matrices:
In optimal alignment procedures, mostly Needleman-Wunsch and Smith-Waterman algorithms use scoring system. For nucleotide sequence alignment, the scoring matrices used are relatively simpler since the frequency of mutation for all the bases are equal. Positive or higher value is assigned for a match and a negative or a lower value is assigned for mismatch. These assumption based scores can be used for scoring the matrices. There are other scoring matrices which are predefined mostly, used in the case of amino acid substitutions.
Mainly used predefined matrices are PAM and BLOSUM.
PAM Matrices: Margaret Dayhoff was the first one to develop the PAM matrix, PAM stands for Point Accepted Mutations. PAM matrices are calculated by observing the differences in closely related proteins. One PAM unit (PAM1) specifies one accepted point mutation per 100 amino acid residues, i.e. 1% change and 99% remains as such.
BLOSUM: BLOcks SUbstitution Matrix, developed by Henikoff and Henikoff in 1992, used conserved regions. These matrices are actual percentage identity values. Simply to say, they depend on similarity. Blosum 62 means there is 62 % similarity.
Gap score or gap penalty: Dynamic programming algorithms use gap penalties to maximize the biological meaning. Gap penalty is subtracted for each gap that has been introduced. There are different gap penalties such as gap open and gap extension. The gap score defines a penalty given to alignment when we have insertion or deletion. During the evolution, there may be a case where we can see continuous gaps all along the sequence, so the linear gap penalty would not be appropriate for the alignment. Thus gap open and gap extension has been introduced when there are continuous gaps (five or more). The open penalty is always applied at the start of the gap, and then the other gaps following it is given with a gap extension penalty which will be less compared to the open penalty. Typical values are –12 for gap opening, and –4 for gap extension.
Working of Needleman -Wunsch Algorithm
To study the algorithm, consider the two given sequences.
CGTGAATTCAT (sequence #1) , GACTTAC (sequence #2)
The length (count of the nucleotides or amino acids) of the sequence 1 and sequence 2 are 11 and 7 respectively. The initial matrix is created with A+1 column’s and B+1 row’s (where A and B corresponds to length of the sequences). Extra row and column is given, so as to align with gap, at the starting of the matrix as shown in Figure 1.
Figure 1: Initial matrix
After creating the initial matrix, scoring schema has to be introduced which can be user defined with specific scores. The simple basic scoring schema can be assumed as, if two residues (nucleotide or amino acid) at ith and jth position are same, matching score is 1 (S(i,j)= 1) or if the two residues at ith and jth position are not same, mismatch score is assumed as -1 (S(i,j)= -1 ). The gap score(w) or gap penalty is assumed as -1 .
*Note: The scores of match, mismatch and gap can be user defined, provided the gap penalty should be negative or zero.
Gap score is defined as penalty given to alignment, when we have insertion or deletion.
The dynamic programming matrix is defined with three different steps.
1.Initialization Step
This example assumes that there is gap penalty. First row and first column of the matrix can be initially filled with 0. If the gap score is assumed, the gap score can be added to the previous cell of the row or column (Figure 2).
Figure 2: Initialization of matrix
2.Matrix Fill Step
The second and crucial step of the algorithm is matrix filling starting from the upper left hand corner of the matrix. To find the maximum score of each cell, it is required to know the neighbouring scores (diagonal, left and right) of the current position. From the assumed values, add the match or mismatch (assumed) score to the diagonal value. Similarly add the gap score to the other neighbouring values. Thus, we can obtain three different values, from that take the maximum among them and fill the ith and jth position with the score obtained.
In terms of matrix positions, it is important to know [M(i-1,j-1)+S(i,j),M(i,j-1)+w,M(i-1,j)+w]
Overall the equation can be showed in the following manner
To score the matrix of the current position (the first position M1,1) the above stated formulae can be used. The first residue (nucleotides or amino acids) in the 2 sequences are ‘G’ and ‘C’. Since they are mismatching residues, the score would (Si,j=- 1) be -1.
= = =
The obtained score -1 is placed in position i,j (1,1) of the scoring matrix. Similarly using the above equation and method, fill all the remaining rows and columns. Place the back pointers to the cell from where the maximum score is obtained, which are predecessors of the current cell (Figure 3).
Figure 3: Matrix filling with back pointers
3.Trace back Step
The final step in the algorithm is the trace back for the best alignment. In the above mentioned example, one can see the bottom right hand corner score as -1. The important point to be noted here is that there may be two or more alignments possible between the two example sequences.
By continuing the trace back step by the above defined method, one would reach to the 0th row, 0th column. Following the above described steps, alignment of two sample sequences can be found. The best alignment among the alignments can be identified by using the maximum alignment score (match =5, mismatch=-1, gap=-2) which may be user defined (Figure 4).
Figure 4: The possible Alignments with trace backing
Cite this Simulator: |
..... | ||
| ..... | ..... | |||
 |
Copyright @ 2024 Under the NME ICT initiative of MHRD |
 |

.jpg)
.jpg)
![Double click to edit «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi»M«/mi»«mrow»«mi»i«/mi»«mo»,«/mo»«mi»j«/mi»«/mrow»«/msub»«mo»§nbsp;«/mo»«mo»=«/mo»«mo»§nbsp;«/mo»«mi»M«/mi»«mi»a«/mi»«mi»x«/mi»«mi»i«/mi»«mi»m«/mi»«mi»u«/mi»«mi»m«/mi»«mo»§nbsp;«/mo»«mfenced close=¨]¨ open=¨[¨»«mrow»«msub»«mi»M«/mi»«mrow»«mi»i«/mi»«mo»-«/mo»«mn»1«/mn»«mo»,«/mo»«mi»j«/mi»«mo»-«/mo»«mn»1«/mn»«/mrow»«/msub»«mo»§nbsp;«/mo»«mo»+«/mo»«mo»§nbsp;«/mo»«msub»«mi»S«/mi»«mrow»«mi»i«/mi»«mo»,«/mo»«mi»j«/mi»«/mrow»«/msub»«mo»,«/mo»«mo»§nbsp;«/mo»«msub»«mi»M«/mi»«mrow»«mi»i«/mi»«mo»,«/mo»«mi»j«/mi»«mo»-«/mo»«mn»1«/mn»«/mrow»«/msub»«mo»§nbsp;«/mo»«mo»+«/mo»«mo»§nbsp;«/mo»«mi»W«/mi»«mo»,«/mo»«mo»§nbsp;«/mo»«msub»«mi»M«/mi»«mrow»«mi»i«/mi»«mo»-«/mo»«mn»1«/mn»«mo»,«/mo»«mi»j«/mi»«/mrow»«/msub»«mo»+«/mo»«mi»W«/mi»«/mrow»«/mfenced»«/math»](/fckeditor/editor/plugins/fckeditor_wiris/integration/showimage.php?formula=b6d905f2c8a8573692f67cf1e8db8f67.png)
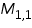 =
= ![Double click to edit «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»M«/mi»«mi»a«/mi»«mi»x«/mi»«mo»§nbsp;«/mo»«mfenced close=¨]¨ open=¨[¨»«mrow»«msub»«mi»M«/mi»«mrow»«mn»0«/mn»«mo»,«/mo»«mn»0«/mn»«/mrow»«/msub»«mo»§nbsp;«/mo»«mo»+«/mo»«mo»§nbsp;«/mo»«msub»«mi»S«/mi»«mrow»«mn»1«/mn»«mo»,«/mo»«mn»1«/mn»«/mrow»«/msub»«mo»,«/mo»«mo»§nbsp;«/mo»«msub»«mi»M«/mi»«mrow»«mn»1«/mn»«mo»,«/mo»«mn»0«/mn»«/mrow»«/msub»«mo»§nbsp;«/mo»«mo»+«/mo»«mi»W«/mi»«mo»,«/mo»«mo»§nbsp;«/mo»«msub»«mi»M«/mi»«mrow»«mn»0«/mn»«mo»,«/mo»«mn»1«/mn»«/mrow»«/msub»«mo»+«/mo»«mi»W«/mi»«/mrow»«/mfenced»«/math»](/fckeditor/editor/plugins/fckeditor_wiris/integration/showimage.php?formula=31f2b0fe661cbb913155623838dc7eeb.png)
![Double click to edit «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»M«/mi»«mi»a«/mi»«mi»x«/mi»«mo»§nbsp;«/mo»«mfenced close=¨]¨ open=¨[¨»«mrow»«mn»0«/mn»«mo»+«/mo»«mfenced»«mrow»«mo»-«/mo»«mn»1«/mn»«/mrow»«/mfenced»«mo»,«/mo»«mo»§nbsp;«/mo»«mn»0«/mn»«mo»§nbsp;«/mo»«mo»+«/mo»«mfenced»«mrow»«mo»-«/mo»«mn»1«/mn»«/mrow»«/mfenced»«mo»,«/mo»«mn»0«/mn»«mo»+«/mo»«mfenced»«mrow»«mo»-«/mo»«mn»1«/mn»«/mrow»«/mfenced»«/mrow»«/mfenced»«/math»](/fckeditor/editor/plugins/fckeditor_wiris/integration/showimage.php?formula=017d07a587aa7a2402984978be67d609.png)
![Double click to edit «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»M«/mi»«mi»a«/mi»«mi»x«/mi»«mfenced close=¨]¨ open=¨[¨»«mrow»«mo»-«/mo»«mn»1«/mn»«mo»,«/mo»«mo»-«/mo»«mn»1«/mn»«mo»,«/mo»«mo»-«/mo»«mn»1«/mn»«/mrow»«/mfenced»«/math»](/fckeditor/editor/plugins/fckeditor_wiris/integration/showimage.php?formula=b0338564729e2e6cc65e5c874975481b.png)
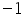
.jpg)
.jpg)