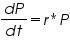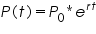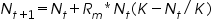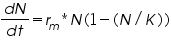| . | . | |||
| . | Logistic Population Growth: Continuous and Discrete |
. | ||
| . | Objectives:
1) To study the rate of population growth in a constrained environment. 2) To explore various aspects of logistic population growth models, such as growth rate and carrying capacity. 3) To understand discrete and continuous growth models using mathematically defined equations.
Carrying Capacity: The largest population that can be supported indefinitely, given the resources available in the environment.
Here we attempt to study the population dynamics, when they are subjected to constraints like limited food supply, etc. We also study these dynamics while considering the existence of intraspecific competition (competition between the individuals of the same species). Such type of population growth is termed as logistic growth. Logistic growth assumes that systems grow exponentially until an upper limit or "carrying capacity" inherent in the system approaches, at which point the growth rate slows and eventually saturates, producing the characteristic S-shape curve (Stone, 1980). Logistic models are density dependent where the growth rate is equal to the birth rate minus the death rate.
When a population is provided with plenty of food, space to grow, and no threat from predators, it tends to grow at a rate that is proportional to the population-that is, in each unit of time, a certain percentage of individuals produce new individuals. Where P is the population as a function of time t, and r is the proportionality constant. All natural growth equations have the form of
Most populations are constrained by limitations on resources but cannot be constrained forever. The figure below (Fig. 1) shows two possible courses for growth of a population, the magenta curve following an exponential (unconstrained) pattern, the orange curve constrained so that the population is always less than some number K. When the population is small relative to K, the two patterns are virtually identical-that is, the constraint doesn't make much difference. But, for the second population, as P becomes a significant fraction of K, the curves begin to diverge, and as P gets close to K, the growth rate drops to 0. The logistic equation is a simple model of population growth in conditions where there are limited resources. When the population is low it grows in an approximately exponential way. Then, as the effects of limited resources become important, the growth slows, and approaches a limiting value, the equilibrium population or carrying capacity.
Figure. 1
Logistic equation is parabolic like the quadratic mapping with f(0)=f(1)=0. Behavior of the logistic equation is more complex than that of the simple harmonic oscillator. The type of orbit depends on the growth rate of parameter, but in a manner that does not lend itself to "less than", "greater than", "equal to" statements. The best way to visualize the behavior of the orbits as a function of the growth rate is with a bifurcation diagram. Logistic growth model is a S-shaped curve. In biology and other fields, many processes exhibit S-shaped growth. Usually the curves are well modeled by the simple logistic growth function, which was first introduced by Verhulst in 1845. Kingsland provided a thorough history of the applications of the simple logistic curve in population ecology, its successes and failures.
Logistic growth can be explained in either continuous or discrete fashion.
Discrete Growth:
The logistic equation assumes that the expected number of offspring decreases linearly with population size. The equation for the logistic growth follows as below:
Here, Nt+1 refers to the number of individuals in next generation,
Where, the term (K-Nt)/K is nearly equal to K/K or 1. The model will then behave like a geometric model, and the population will grow, provided R>1. The population will grow slowly at first, because the parameter R is also being multiplied by a number (Nt) that is nearly equal to zero, but it will grow faster and faster, at least for a while. At some point, however, population growth will begin to slow because the term (K-Nt)/K is getting smaller and smaller as Nt gets larger and closer to K. The discrete equation shows that the behavior of a population is jointly determined by Rm and K, the per capita rate of increase and the population's carrying capacity. The behavior of the population is seen as being jointly determined by two properties of the individuals within it-their intrinsic per capita rate of increase and their susceptibility to crowding, Ra and a. The carrying capacity of the population (K=(R-1)/a) is then simply the outcome for these properties.
Continuous Growth:
The model of logistic growth in continuous time follows from the assumption that each individual reproduces at a rate that decreases as a linear function of the population size. The equation for the continuous time model is shown below:
Here, rm is the maximum rate of growth, N is the number of individuals, K is the carrying capacity.
Population sizes that are less than K, the population will increase in size: at population sizes that are greater than K the population size will decline; and at K itself the population neither increases nor decreases. The carrying capacity is therefore a stable equilibrium for the population, and the model exhibits the regulatory properties classically characteristic of intraspecific competition. For the continuous time model, birth and death are continuous. The net rate of such a population will be denoted by dN/dt. This represents the 'speed' at which a population increases in size, N, as time, t, progresses. It describes a sigmoidal growth curve approaching a stable carrying capacity, but it is only one of many reasonable equation that do this (see Fig. 2).  Fig. 2
1) If K were infinity, N[t]/K would be zero and the population growth would follow the equation for exponential growth.
2) If the population size, N[t] were much smaller than carrying capacity K then N[t]/K would be small. In this case the population would grow nearly exponentially (until the population size were no longer much smaller than K).
Note:
|
..... | ||
| ..... | ..... | |||
 |
Copyright @ 2025 Under the NME ICT initiative of MHRD |
 |