
| . | . | |||
| . | Ebullioscopy |
. | ||
| . | Objectives:1. To understand colligative properties of solutes.
2. To find the boiling point elevation of a solution.
3. To determine the van ‘t Hoff factor of solutes.
4. To find the molar mass of an unknown solute.
Theory:Ebullioscopy:
The boiling point of a liquid is the temperature at which its vapour pressure becomes equal to the external atmospheric pressure. The phenomenon that the boiling point of a solvent will be higher when another compound is added is known as Boiling point elevation, ie., the boiling point of a pure solvent will always less than its solution. The boiling point of a substance can be measured by using ebullioscopy. The addition of a non-volatile solute to pure solvent increases the boiling point of the solution. The difference between the boiling points of the solution,
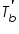 and the pure solvent, and the pure solvent, 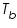 is called elevation of boiling point of the solvent. is called elevation of boiling point of the solvent.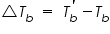 This is a colligative property which does not depend on the nature of solute particles but depend only on the number of those solute particles in solution. The elevation of the boiling point can be calculated by applying the assumption of the non-volatility of the solute together with the Clausius-Clapeyron relation and Raoult’s law.
Raoult's law:
The vapour pressure of a solution of a non-volatile solute is equal to the product of the vapour pressure of the pure solvent at that temperature and its mole fraction.
In equilibrium, the total vapour pressure , ‘
 ’ of the solution is: ’ of the solution is: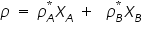 As the number of components in a solution increases, the individual vapour pressure decreases, i.e. the mole fraction of each component is indirectly proportional to each additional component and is individual vapour pressure for each component is:
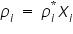 Where, 

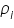 is the partial pressure of the component i in the solution; is the partial pressure of the component i in the solution; 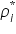 is the vapour pressure of the pure component i; and is the vapour pressure of the pure component i; and 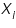 is the mole fraction of the component i in the solution (in mixture). is the mole fraction of the component i in the solution (in mixture).Therefore the vapour pressure of the final solution will be lower than that of the pure solvent as given by the following equation:
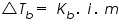 Where,
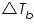 is the elevation of the boiling point;
m is the molality of the solution; and i is the van ‘t Hoff factor. Molality of a solution is the ratio of amount of substance of solute and the mass of solvent in kg. is the elevation of the boiling point;
m is the molality of the solution; and i is the van ‘t Hoff factor. Molality of a solution is the ratio of amount of substance of solute and the mass of solvent in kg.The value of van ‘t Hoff factor depends upon the number of individual ions formed in solution. i.e:
· i = 1 for sugar in water.
· i = 2 for sodium chloride (NaCl) in water, due to the its full dissociation into Na+ and Cl- ions.
· i = 3 for calcium chloride (CaCl2) in water, due to its full dissociation Ca2+ and 2Cl- ions.
The van ‘t Hoff factor is a measure of the colligative effect (the total number of particles) of the solute in solution. The value of i is usually unity for all non-electrolytes, greater than unity for electrolytes, but is less than unity for compounds that associate in solution.
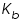 is the molal boiling point elevation constant or ebullioscopic constant of the solvent, and it is depends upon the properties of the solvent. Which can be calculated as: is the molal boiling point elevation constant or ebullioscopic constant of the solvent, and it is depends upon the properties of the solvent. Which can be calculated as: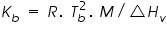 Calculation of molecular mass of a solute from elevation of boiling point:
It is possible to calculate the molecular mass of a solute from the observed elevation in the boiling point by using the equation:
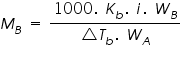 Where,
 is the weight of the solute; is the weight of the solute; is the weight of solvent; 
 is the weight of solvent; 
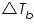 is the elevation of the boiling point; is the elevation of the boiling point; 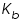 molal boiling point elevation constant; and i is the van ‘t Hoff factor. molal boiling point elevation constant; and i is the van ‘t Hoff factor. Chemical potential of a solvent changes when a solute is added and this explains the elevation in boiling point.
Cite this Simulator: |
..... | ||
| ..... | ..... | |||
 |
Copyright @ 2024 Under the NME ICT initiative of MHRD |
 |
Powered by AmritaVirtual Lab Collaborative Platform [ Ver 00.13. ]
