
| . | . | |||||||||||||||||||||||
| . | Exp-4 Sampling and signal reconstruction. |
. | ||||||||||||||||||||||
| . |
♦ Nyquist sampling theorem ♦ Sampling of non-bandlimited signal (anti-aliasing filter) ♦ Signal reconstruction ♦ Zero-order hold ♦ First-order hold ♦ The discrete Fourier transform ♦ Picket-fence effect ♦ Properties of discrete Fourier transform
-- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ -- ♦ --
Sampling:
A continuous time signal can be processed by processing its samples through a discrete time system. For reconstructing the continuous time signal from its discrete time samples without any error, the signal should be sampled at a sufficient rate that is determined by the sampling theorem.
If a signal is band limited and its samples are taken at sufficient rate then those samples uniquely specify the signal and the signal can be reconstructed from those samples. The condition in which this is possible is known as Nyquist sampling theorem and is derived below. A real signal whose spectrum is bandlimited to D Hz [X(f) = 0 for | f |>D] can be reconstructed from its samples taken uniformly at a rate fs > 2D samples/sec. We can say the minimum sampling frequency is fs=2D Hz. Consider a signal x(t) as shown in Fig.1 and its spectrum is shown in Fig.2 which is noted to be bandlimited to D=1 Hz . Sampling x(t) at a rate of fs Hz, (means fs samples/sec) can be mathematically represented as multiplying x(t) by an impulse train
The sampled signal consists of impulses spaced every T seconds. The nth impulse, located at t = nT, has a strength x(nT), the value of x(t) at t = nT, Since the impulse train where Therefore To find X'(f), the Fourier transform of x'(t), we take the Fourier transform of the right hand side of the above equation, term by term. The transform of the first term in the bracket of the above equation (3) is X(f). Similarly the transform of the second term If we want to reconstruct x(t) from x'(t), we should be able to recover X(f) from X'(f). This recovery is possible if there is no overlap between successive cycles of X'(f). From Fig.4 we noted that for no overlap between successive cycle of X'(f) we should have Thus as long as the sampling frequency fs is greater than twice the signal bandwidth D (in Hz), X'(f) will consist of nonoverlapping repetitions of X(f). In such a case it indicates that x(t) can be recovered from its samples x'(t) by passing the sampled signal x'(t) through an ideal low pass filter of bandwidth D Hz. If a signal is sampled with a sampling frequency fs which is below the highest frequency present in the signal then the signal is called undersampled signal and if the signal is sampled with a sampling frequency fs which is slightly higher than twice the bandwidth of the signal or highest frequency present in the signal then the signal is called oversampled signal.
In reconstructing a signal from its samples, there is another practical difficulty. The sampling theorem was proved on the assumption that the signal x(t) is bandlimited. All practical signals are time limited, i.e., they are of finite duration. As a signal cannot be timelimited and bandlimited simultaneously. Thus, if a signal is timelimited, it cannot be bandlimited and vice versa (but it can be simultaneously non timelimited and non bandlimited). Clearly it can be said that all practical signals which are necessaily timelimited, are non bandlimited, they have infinite bandwidth and the spectrum X'(f) consists of overlapping cycles of X(f) repeating every fs Hz (sampling frequency). Because of infinite bandwidth, the spectral overlap will always be present regardless of what ever may be the sampling rate chosen. Because of the overlapping tails, X'(f) has not complete information about X(f) and it is not possible, even theoretically to recover x(t) from the sampled signal x'(t). If the sampled signal is passed through an ideal lowpass filter, the output is not X(f) but a version of X(f) distorted as a result of some causes:
Sampling of Non-bandlimited Signal: Anti-aliasing Filter
Anti aliasing filter is a filter which is used before a signal sampler, to restrict the bandwidth of a signal to approximately satisfy the sampling theorem. The potential defectors are all the frequency components beyond fs/2 Hz. We should have to eliminate these components from x(t) before sampling x(t). As a result of this we lose only the components beyond the folding frequency fs/2 Hz. These frequency components cannot reappear to corrupt the components with frequencies below the folding frequency. This suppression of higher frequencies can be accomplished by an ideal filter of bandwidth fs/2 Hz. This filter is called the anti-aliasing filter. The anti aliasing operation must be performed before the signal is sampled. The anti aliasing filter, being an ideal filter is unrealizable. In practice, we use a steep cutoff filter, which leaves a sharply attenuated residual spectrum beyond the folding frequency fs/2.
The process of reconstructing a continuous time signal x(t) from its samples is known as interpolation. In the sampling theorem we saw that a signal x(t) band limited to D Hz can be reconstructed from its samples. This reconstruction is accomplished by passing the sampled signal through an ideal low pass filter of bandwidth D Hz. As seen in the above equation(3), the sampled signal contains a component The description of the process of reconstruction in the frequency domain is to find the DTFT of the discrete-time signal, change the variable F→f / fs , multiply by T and find the inverse CTFT. We find the DTFT from the samples using Here we are using the notations X(f) for CTFT and X(F) for DTFT.
For sinc function, the DTFT is illustrated in Fig.6. To isolate the function indexed by k = 0, we can multiply the DTFT by a rectangle function that is wide enough to include the k = 0 alias but not wide enough to include any other aliases. So the corner of the rectangle must be at a value of F which is greater than Fm= fm/ fs, where fm is the highest frequency present in the signal x(t) but less than 1 - Fm or more compactly, Fm< Fc<1 - Fm. The isolated k = 0 replica is then Next we make the change of variable F→ f / fs and multiply it by T Now we have to find out the inverse CTFT, which is Let Fc = fc/fs , then By exchanging the order of integration and summation we can recognize the integrand as a time shifted inverse CTFT of a frequency domain rectangle function. Then x[n] = x(nT), The reconstruction process consists of replacing each sample by a sinc function, centered at the time of the sample and scaled by the sample value x(nT) times 2fc/ fs and adding all the functions so created. Suppose the signal is sampled at exactly Nyquist rate fs= 2fm, Then fm= fs/2 = fs- fm and Fm= 1/2 = 1- Fm. The requirement Fm< Fc< 1- Fm cannot be met, in this case we must allow Fc= Fm, which means that fc= fm= fs/2 This will work till the signals spectrum does not have an impulse at fm. (If there is an impulse at fm , it will be aliased in the sampling process). In this limiting case, the interppolation is described by the simpler expression Interpolation consists of simply of multiplying each sinc function by its corresponding sample value and then adding all the scaled and shifted sinc functions as shown in Fig.7 given below.
The interpolated value at any point is the sum of contributions from infinitely many weighted sinc functions.
There are many techniques that can be used to reconstruct a signal and the selection of the technique to be used is depends on what accuracy of reconstruction is required and how oversampled the signal is. Probably the simplest approximate reconstruction idea is to simply let the reconstruction always be the value of the most recent sample as shown in Figure 8. Fig.8 Zero order hold signal reconstruction. Fig.9 Impulse response of a Zero order hold.
It is a simple technique because the samples in the form of numerical codes, can be the input signal to a Digital to Analog converter, which is clocked to produce a new output signal with every clock pulse. This technique produces a signal which has a stair step shape that follows the original signal. This type of signal reconstruction can be modeled (except for quantization effects) by passing the impulse sampled signal through a system called a zero order hold whose impulse response is
which is shown in Figure 9.
One popular way of further reducing the effects of the aliases is to follow the zero order hold with a practical lowpass filter that smooths out the steps caused by the zero order hold. The zero order hold causes a delay to the original signal because it is causal. Another natural reconstruction idea is to interpolate between samples with straight lines as shown in Fig.10 below. This is obviously a better approximation of the original signal but it is a little harder to implement.
Fig.10 Signal reconstruction by straight-line interpolation. Fig.11 Impulse response of causal first-order hold.
As shown in above figure the value of the interpolated signal at any time depends on the value of the previous sample and the value of the next sample and this is not possible in real time because the value of the next sample is not known in real time. But if we delay the reconstructed signal by one sample time T, we can make the reconstruction process causal and the reconstructed signal would appear as like the Figure 12.
Fig.12 Straight line signal reconstruction delayed by one sample time
This interpolation can be accomplished by following the zero order hold by an identical zero order hold. This means that the impulse response of such a signal reconstruction filter would be the convolution of the zero order hold impulse response with itself
This type of filter is called first order hold. Its transfer function is
The discrete Fourier transform (DFT): If x(kT) and X(rf0) are the kth and rth samples of x(t) and X(f) respectively, then we can define new variables xk and Xr as and Xr = X(rf0) where We will now see that xk and Xr are related by the following equation DFT, and IDFT Here Xr is the discrete Fourier transform of 'xk' and 'xk' is the IDFT of Xr . The notation xk ⇆Xr is also used to indicate that xk and Xr are a DFT pair. Remember that xk is T0/ N0 times the kth sample of x(t) and Xr is the rth sample of X(f).
The numerical computation method yields only the uniform sample values of X(f) or x(t). Using this method is like viewing a signal and its spectrum through a "picket fence". The major peaks of X(f) or x(t) could lie between two samples and may remain hidden, there is a situation giving a false picture of the reality. Such misleading results can be avoided by using a sufficiently large 'N0' the no. of samples, which increases the resolution.
Observing Xr is like observing the spectrum X(f) through a "picket-fence". If the frequency sampling interval f0 is not sufficiently small, we could miss out some significant details and obtain a misleading picture. To obtain a higher number of samples, we need to reduce f0. Because f0 = 1/T0, a higher number of samples requires us to increase the value of 'T0' the period of repetition for x(t). This option increases 'N0' the number of samples of x(t), by adding samples with a value of 0. This addition of dummy samples is known as zero padding. zero padding increases the number of samples and it may help in getting a better idea of the spectrum X(f) from its samples Xr.
Properties of discrete Fourier transform:
The DFT is basically the Fourier transform of the sampled signal which is repeated periodically. So the properties of the Fourier transform can also applied for DFT. 1. Linearity property: If 2. Time shifting (Circular shifting): 3. Frequency shifting: 4. Circular convolution: For two 'N0' periodic sequences xk and 'gk' the circular convolution is defined as
Cite this Simulator: |
..... | ||||||||||||||||||||||
| ..... | ..... | |||||||||||||||||||||||
 |
Copyright @ 2025 Under the NME ICT initiative of MHRD |
 |







 ..............(1)
..............(1)![Double click to edit «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi»§#948;«/mi»«mi»T«/mi»«/msub»«mo»(«/mo»«mi»t«/mi»«mo»)«/mo»«mo»=«/mo»«mfrac»«mn»1«/mn»«mi»T«/mi»«/mfrac»«mo»[«/mo»«mn»1«/mn»«mo»+«/mo»«mn»2«/mn»«mi mathvariant=¨normal¨»cos«/mi»«msub»«mi»§#969;«/mi»«mi»s«/mi»«/msub»«mi»t«/mi»«mo»+«/mo»«mn»2«/mn»«mi mathvariant=¨normal¨»cos«/mi»«mn»2«/mn»«msub»«mi»§#969;«/mi»«mi»s«/mi»«/msub»«mi»t«/mi»«mo»+«/mo»«mn»2«/mn»«mi mathvariant=¨normal¨»cos«/mi»«mn»3«/mn»«msub»«mi»§#969;«/mi»«mi»s«/mi»«/msub»«mi»t«/mi»«mo»+«/mo»«mo».«/mo»«mo».«/mo»«mo».«/mo»«mo»]«/mo»«/math»](http://iitg.vlab.co.in/fckeditor/editor/plugins/fckeditor_wiris/integration/showimage.php?formula=592a0a66336fbc6c424193a5653c2930.png) ................(2)
................(2) 
![Double click to edit «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»x«/mi»«mo»§apos;«/mo»«mo»(«/mo»«mi»t«/mi»«mo»)«/mo»«mo»=«/mo»«mi»x«/mi»«mo»(«/mo»«mi»t«/mi»«mo»)«/mo»«msub»«mi»§#948;«/mi»«mi»T«/mi»«/msub»«mo»(«/mo»«mi»t«/mi»«mo»)«/mo»«mo»=«/mo»«mfrac»«mn»1«/mn»«mi»T«/mi»«/mfrac»«mo»[«/mo»«mi»x«/mi»«mo»(«/mo»«mi»t«/mi»«mo»)«/mo»«mo»+«/mo»«mn»2«/mn»«mi»x«/mi»«mo»(«/mo»«mi»t«/mi»«mo»)«/mo»«mi mathvariant=¨normal¨»cos«/mi»«msub»«mi»§#969;«/mi»«mi»s«/mi»«/msub»«mi»t«/mi»«mo»+«/mo»«mn»2«/mn»«mi»x«/mi»«mo»(«/mo»«mi»t«/mi»«mo»)«/mo»«mi mathvariant=¨normal¨»cos«/mi»«mn»2«/mn»«msub»«mi»§#969;«/mi»«mi»s«/mi»«/msub»«mi»t«/mi»«mo»+«/mo»«mn»2«/mn»«mi»x«/mi»«mo»(«/mo»«mi»t«/mi»«mo»)«/mo»«mi mathvariant=¨normal¨»cos«/mi»«mn»3«/mn»«msub»«mi»§#969;«/mi»«mi»s«/mi»«/msub»«mo»(«/mo»«mi»t«/mi»«mo»)«/mo»«mo»+«/mo»«mo».«/mo»«mo».«/mo»«mo».«/mo»«mo».«/mo»«mo».«/mo»«mo».«/mo»«mo».«/mo»«mo»]«/mo»«/math»](http://iitg.vlab.co.in/fckeditor/editor/plugins/fckeditor_wiris/integration/showimage.php?formula=a781ada213f5a31f2ce0e00a42f7204e.png) .........(3)
.........(3) is
is . This represents spectrum X(f) shifted to
. This represents spectrum X(f) shifted to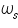 and
and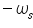 and so on to infinity. This result means that the spectrum X'(f) consists of X(f) repeating periodically with period
and so on to infinity. This result means that the spectrum X'(f) consists of X(f) repeating periodically with period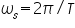 rad/s, or fs =1/T Hz, as shown in Fig.4. Therefore
rad/s, or fs =1/T Hz, as shown in Fig.4. Therefore
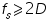 or
or 


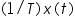 and to recover x(t) or X(f), the sampled signal must be passed through an ideal lowpass filter having bandwidth D Hz and gain T.
and to recover x(t) or X(f), the sampled signal must be passed through an ideal lowpass filter having bandwidth D Hz and gain T.![Double click to edit «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»X«/mi»«mo»(«/mo»«mi»F«/mi»«mo»)«/mo»«mo»=«/mo»«munderover»«mo»§#8721;«/mo»«mrow»«mi»n«/mi»«mo»=«/mo»«mo»-«/mo»«mo»§#8734;«/mo»«/mrow»«mo»§#8734;«/mo»«/munderover»«mi»x«/mi»«mo»[«/mo»«mi»n«/mi»«mo»]«/mo»«msup»«mi»e«/mi»«mrow»«mo»-«/mo»«mi»j«/mi»«mn»2«/mn»«mi»§#960;«/mi»«mi»F«/mi»«mi»n«/mi»«/mrow»«/msup»«/math»](http://iitg.vlab.co.in/fckeditor/editor/plugins/fckeditor_wiris/integration/showimage.php?formula=7bd653ef39b1b5064e4a8b47ec159adc.png)
![Double click to edit «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«msub»«mi»X«/mi»«mrow»«mi»F«/mi»«mn»0«/mn»«/mrow»«/msub»«mo»(«/mo»«mi»F«/mi»«mo»)«/mo»«mo»=«/mo»«mi mathvariant=¨normal¨»rect«/mi»«mo»(«/mo»«mfrac»«mi»F«/mi»«mrow»«mn»2«/mn»«msub»«mi»F«/mi»«mi»c«/mi»«/msub»«/mrow»«/mfrac»«mo»)«/mo»«munderover»«mo»§#8721;«/mo»«mrow»«mi»n«/mi»«mo»=«/mo»«mo»-«/mo»«mo»§#8734;«/mo»«/mrow»«mo»§#8734;«/mo»«/munderover»«mi»x«/mi»«mo»[«/mo»«mi»n«/mi»«mo»]«/mo»«msup»«mi»e«/mi»«mrow»«mo»-«/mo»«mi»j«/mi»«mn»2«/mn»«mi»§#960;«/mi»«mi»F«/mi»«mi»n«/mi»«/mrow»«/msup»«/math»](/fckeditor/editor/plugins/fckeditor_wiris/integration/showimage.php?formula=99254b7d61883cdc0af5a18c3ba66591.png)
![Double click to edit «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»X«/mi»«mo»(«/mo»«mi»f«/mi»«mo»)«/mo»«mo»=«/mo»«mi»T«/mi»«msub»«mi»X«/mi»«mrow»«mi»F«/mi»«mn»0«/mn»«/mrow»«/msub»«mo»(«/mo»«mfrac»«mi»f«/mi»«msub»«mi»f«/mi»«mi»s«/mi»«/msub»«/mfrac»«mo»)«/mo»«mo»=«/mo»«mi»T«/mi»«mo»§nbsp;«/mo»«mi mathvariant=¨normal¨»rect«/mi»«mo»(«/mo»«mo»(«/mo»«mfrac»«mi»f«/mi»«msub»«mi»f«/mi»«mi»s«/mi»«/msub»«/mfrac»«mo»)«/mo»«mo»/«/mo»«mn»2«/mn»«msub»«mi»F«/mi»«mi»c«/mi»«/msub»«mo»)«/mo»«munderover»«mo»§#8721;«/mo»«mrow»«mi»n«/mi»«mo»=«/mo»«mo»-«/mo»«mo»§#8734;«/mo»«/mrow»«mo»§#8734;«/mo»«/munderover»«mi»x«/mi»«mo»[«/mo»«mi»n«/mi»«mo»]«/mo»«msup»«mi»e«/mi»«mrow»«mo»-«/mo»«mi»j«/mi»«mn»2«/mn»«mi»§#960;«/mi»«msub»«mi»f«/mi»«mi»n«/mi»«/msub»«mo»/«/mo»«msub»«mi»f«/mi»«mi»s«/mi»«/msub»«/mrow»«/msup»«/math»](/fckeditor/editor/plugins/fckeditor_wiris/integration/showimage.php?formula=614faee40eccfadb8ca15739b74c7571.png)
![Double click to edit «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»x«/mi»«mo»(«/mo»«mi»t«/mi»«mo»)«/mo»«mo»=«/mo»«msup»«mi»F«/mi»«mrow»«mo»-«/mo»«mn»1«/mn»«/mrow»«/msup»«mo»(«/mo»«mi»X«/mi»«mo»(«/mo»«mi»f«/mi»«mo»)«/mo»«mo»)«/mo»«mo»=«/mo»«msubsup»«mo»§#8747;«/mo»«mrow»«mo»-«/mo»«mo»§#8734;«/mo»«/mrow»«mo»§#8734;«/mo»«/msubsup»«mi»T«/mi»«mo»§nbsp;«/mo»«mi mathvariant=¨normal¨»rect«/mi»«mo»(«/mo»«mo»(«/mo»«mfrac»«mi»f«/mi»«msub»«mi»f«/mi»«mi»s«/mi»«/msub»«/mfrac»«mo»)«/mo»«mo»/«/mo»«mn»2«/mn»«msub»«mi»F«/mi»«mi»c«/mi»«/msub»«mo»)«/mo»«munderover»«mo»§#8721;«/mo»«mrow»«mi»n«/mi»«mo»=«/mo»«mo»-«/mo»«mo»§#8734;«/mo»«/mrow»«mo»§#8734;«/mo»«/munderover»«mi»x«/mi»«mo»[«/mo»«mi»n«/mi»«mo»]«/mo»«msup»«mi»e«/mi»«mrow»«mo»-«/mo»«mi»j«/mi»«mn»2«/mn»«mi»§#960;«/mi»«msub»«mi»f«/mi»«mi»n«/mi»«/msub»«mo»/«/mo»«msub»«mi»f«/mi»«mi»s«/mi»«/msub»«/mrow»«/msup»«msup»«mi»e«/mi»«mrow»«mi»j«/mi»«mn»2«/mn»«mi»§#960;«/mi»«msub»«mi»f«/mi»«mi»t«/mi»«/msub»«/mrow»«/msup»«mi»d«/mi»«mi»f«/mi»«/math»](/fckeditor/editor/plugins/fckeditor_wiris/integration/showimage.php?formula=23cb44a6fcf03c0b1e62d9263816a30d.png)
![Double click to edit «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»x«/mi»«mo»(«/mo»«mi»t«/mi»«mo»)«/mo»«mo»=«/mo»«mi»T«/mi»«msubsup»«mo»§#8747;«/mo»«mrow»«mo»-«/mo»«mo»§#8734;«/mo»«/mrow»«mo»§#8734;«/mo»«/msubsup»«munderover»«mo»§#8721;«/mo»«mrow»«mi»n«/mi»«mo»=«/mo»«mo»-«/mo»«mo»§#8734;«/mo»«/mrow»«mo»§#8734;«/mo»«/munderover»«mi»x«/mi»«mo»[«/mo»«mi»n«/mi»«mo»]«/mo»«mo»§nbsp;«/mo»«mi mathvariant=¨normal¨»rect«/mi»«mo»(«/mo»«mi»f«/mi»«mo»/«/mo»«mn»2«/mn»«msub»«mi»f«/mi»«mi»c«/mi»«/msub»«mo»)«/mo»«msup»«mi»e«/mi»«mrow»«mo»-«/mo»«mi»j«/mi»«mn»2«/mn»«mi»§#960;«/mi»«mi»f«/mi»«mo»(«/mo»«mi»t«/mi»«mo»-«/mo»«mi»n«/mi»«mo»/«/mo»«msub»«mi»f«/mi»«mi»s«/mi»«/msub»«mo»)«/mo»«/mrow»«/msup»«mi»d«/mi»«mi»f«/mi»«/math»](http://iitg.vlab.co.in/fckeditor/editor/plugins/fckeditor_wiris/integration/showimage.php?formula=7d1b1a97562b98a65b9b0f5a4198ab6a.png)
![Double click to edit «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»x«/mi»«mo»(«/mo»«mi»t«/mi»«mo»)«/mo»«mo»=«/mo»«mi»T«/mi»«munderover»«mo»§#8721;«/mo»«mrow»«mi»n«/mi»«mo»=«/mo»«mo»-«/mo»«mo»§#8734;«/mo»«/mrow»«mo»§#8734;«/mo»«/munderover»«mi»x«/mi»«mo»[«/mo»«mi»n«/mi»«mo»]«/mo»«msubsup»«mo»§#8747;«/mo»«mrow»«mo»-«/mo»«mo»§#8734;«/mo»«/mrow»«mo»§#8734;«/mo»«/msubsup»«mi mathvariant=¨normal¨»rect«/mi»«mo»(«/mo»«mfrac»«mi»f«/mi»«mrow»«mn»2«/mn»«msub»«mi»f«/mi»«mi»c«/mi»«/msub»«/mrow»«/mfrac»«mo»)«/mo»«msup»«mi»e«/mi»«mrow»«mo»-«/mo»«mi»j«/mi»«mn»2«/mn»«mi»§#960;«/mi»«mi»f«/mi»«mo»(«/mo»«mi»t«/mi»«mo»-«/mo»«mi»n«/mi»«mi»T«/mi»«mo»)«/mo»«/mrow»«/msup»«mi»d«/mi»«mi»f«/mi»«/math»](/fckeditor/editor/plugins/fckeditor_wiris/integration/showimage.php?formula=a43909a60a75a0550770885b969e1a72.png)
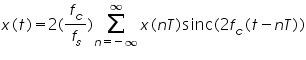




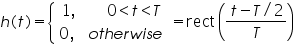




 . This transfer function is similar to that of a zero order hold but attenuates aliases more because its magnitude diminishes faster with increasing frequency.
. This transfer function is similar to that of a zero order hold but attenuates aliases more because its magnitude diminishes faster with increasing frequency.



 and
and  then
then


 and
and 
