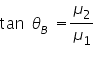| . | . | |||
| . | Brewsters Angle determination |
. | ||
| . |
Aim:
To verify the Brewster's law and to find the Brewster's angle.
Introduction:An ordinary light source consists of a very large number of randomly oriented atomic emitters. They radiate polarized wavetrains for roughly 10-8 s. These wavetrains combine to form a single resultant polarized wave which persists for a short time, not more than 10-8 s. Since natural light composes of a large number of rapidly varying succession of the different polarization states it is said to be an unpolarised or randomly polarized light.
The natural light can be expressed in terms of two arbitrary, incoherent, orthogonal, linearly polarized waves of equal amplitude. Figure (a) shows randomly polarized natural light and figure (b) shows the splitting at 50% horizontal and 50% vertical states.
A light is said to be a plane polarised light, if all the vibrations are confined to a single plane. Consider an unpolarised light incidents on a transparent surface. If the angle of incidence is equal to a particular angle of incidence, the reflected light produced will be completely plane polarized. This particular angle is called the Brewster’s angle or the polarizing angle
|
..... | ||
| ..... | ..... | |||
 |
Copyright @ 2025 Under the NME ICT initiative of MHRD |
 |



 Brewster’s equation:
Brewster’s equation: