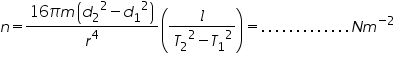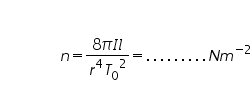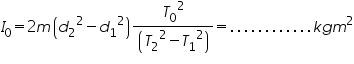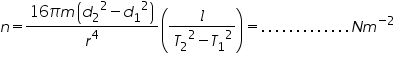Procedure: (for performing in lab)
PART 1: Determination of Rigidity modulus using Torsion pendulum alone
- The radius of the suspension wire is measured using a screw gauge.
- The length of the suspension wire is adjusted to suitable values like 0.3m,0.4m,0.5m,.....0.9m,1m etc.
- The disc is set in oscillation.Find the time for 20 oscillations twice and determine the mean period of oscillation ' T0 '.
- Calculate moment of inertia of the disc using the expression, I = (1/2)MR2.
- Determine the rigidity modulus from the given mathematical expression.
PART 2: Determination of rigidity modulus and moment of inertia using torsion pendulum with identical masses
- The radius of the suspension wire is measured using a screw gauge.
- The length of the suspension wire is adjusted to suitable values like 0.3m,0.4m,0.5m,.....0.9m,1m etc.
- The disc is set in oscillation.Find the time for 20 oscillations twice and determine the mean period of oscillation ' T0 '.
- The two identical masses are placed symmetrically on either side of the suspension wire as close as possible to the centre of the disc, and measure d1 which is the distance between the centres of the disc and one of the identical masses.
- Find the time for 20 oscillations twice and determine the mean period of oscillation ' T1 '.
- The two identical masses are placed symmetrically on either side of the suspension wire as far as possible to the centre of the disc, and measure d2 which is the distance between the centres of the disc and one of the identical masses.
- Find the time for 20 oscillations twice and determine the mean period of oscillation ' T2 '.
- Find the moment of inertia of the disc and rigidity modulus of the suspension wire using the given formulae.
Note: For the same variables of length,mass, etc. the data from part 1 can be used for the Part 2 procedure.
Observations:
Length of the suspension wire=................m
Radius of the suspension wire=..............m
Mass of each identical masses=.............kg
d1=...........m
d2=...........m
For Part 1:

For Part 2:

Calculations:
T0 = ........s
T1 = .........s
T2 = .........s
For Part 1: 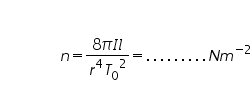
For Part:2
Moment of inertia of the given disc,
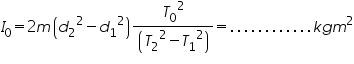
And the rigidity modulus of the suspension wire,