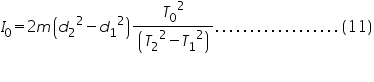Aim:
To determine the moment of inertia of the given disc using Torsion pendulum, with identical masses.
Apparatus:
The given torsion pendulum, two identical cyllindrical masses, stop watch, metre scale, etc.
Theory:
What is Torsional Oscillation?
A body suspended by a thread or wire which twists first in one direction and then in the reverse direction, in the horizontal plane is called a torsional pendulum.The first torsion pendulum was developed by Robert Leslie in 1793.
A simple schematic representation of a torsion pendulum is given below,

The period of oscillation of torsion pendulum is given as,
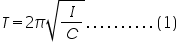
Where I=moment of inertia of the suspended body; C=couple/unit twist
But we have an expression for couple per unit twist C as,
![Double click to edit «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»C«/mi»«mo»=«/mo»«mfrac»«mn»1«/mn»«mn»2«/mn»«/mfrac»«mfrac»«mrow»«mi»§#960;«/mi»«mi»n«/mi»«msup»«mi»r«/mi»«mn»4«/mn»«/msup»«/mrow»«mi»l«/mi»«/mfrac»«mo».«/mo»«mo».«/mo»«mo».«/mo»«mo».«/mo»«mo».«/mo»«mo».«/mo»«mo».«/mo»«mo».«/mo»«mo».«/mo»«mo».«/mo»«mfenced close=¨]¨ open=¨[¨»«mn»2«/mn»«/mfenced»«/math»](http://vlab.amrita.edu/fckeditor/editor/plugins/fckeditor_wiris/integration/showimage.php?formula=77126c04c6f919aa239db3cbeaf63f77.png)
Where l =length of the suspension wire; r=radius of the wire; n=rigidity modulus of the suspension wire
Substituting (2) in (1) and squaring,we get an expression for rigidity modulus for the suspension wire as,

We can use the above formula directly if we calculate the moment of inertia of the disc,I as (1/2)MR2.
Now, let I0 be the moment of inertia of the disc alone and I1 & I2 be the moment of inertia of the disc with identical masses at distances d1&d2 respectively.If I1 is the moment of inertia of each identical mass about the vertical axis passing through its centre of gravity, then
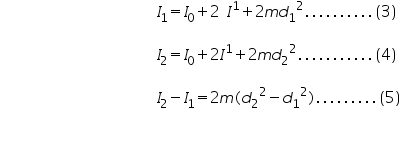
But from equation (1) ,
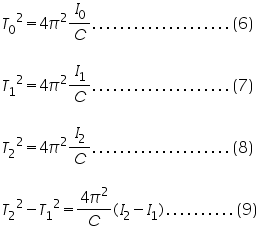
Where T0,T1,T2 are the periods of torsional oscillation without identical mass,with identical pass at position d1,d2 respectively.
Dividing equation (6) by (9) and using (5),
![Double click to edit «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mfrac»«msup»«msub»«mi»T«/mi»«mn»0«/mn»«/msub»«mn»2«/mn»«/msup»«mfenced»«mrow»«msup»«msub»«mi»T«/mi»«mn»2«/mn»«/msub»«mn»2«/mn»«/msup»«mo»-«/mo»«msup»«msub»«mi»T«/mi»«mn»1«/mn»«/msub»«mn»2«/mn»«/msup»«/mrow»«/mfenced»«/mfrac»«mo»=«/mo»«mfrac»«msub»«mi»I«/mi»«mn»0«/mn»«/msub»«mfenced close=¨]¨ open=¨[¨»«mrow»«msub»«mi»I«/mi»«mn»2«/mn»«/msub»«mo»-«/mo»«msub»«mi»I«/mi»«mn»1«/mn»«/msub»«/mrow»«/mfenced»«/mfrac»«mo»=«/mo»«mfrac»«msub»«mi»I«/mi»«mn»0«/mn»«/msub»«mrow»«mn»2«/mn»«mi»m«/mi»«mfenced»«mrow»«msup»«msub»«mi»d«/mi»«mn»2«/mn»«/msub»«mn»2«/mn»«/msup»«mo»-«/mo»«msup»«msub»«mi»d«/mi»«mn»1«/mn»«/msub»«mn»2«/mn»«/msup»«/mrow»«/mfenced»«/mrow»«/mfrac»«mo».«/mo»«mo».«/mo»«mo».«/mo»«mo».«/mo»«mo».«/mo»«mo».«/mo»«mo».«/mo»«mo».«/mo»«mo».«/mo»«mfenced»«mn»10«/mn»«/mfenced»«/math»](http://vlab.amrita.edu/fckeditor/editor/plugins/fckeditor_wiris/integration/showimage.php?formula=03f484acad41c80a8602e81b449f292b.png)
Therefore, the moment of inertia of the disc,