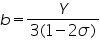AIM:
To find the elastic constants of the Perspex beam using Cornus interference method.
1. Young’s modulus(Y)
2. Poisons ratio (ÃÂÆ’)
3. Bulk modulus (b)
APPARATUS
Sodium vapor lamp, transparent beam, convex lens, travelling microscope, two knife edges, a set of weights, weight holders and a mirror.
EXPERIMENTAL SET UP
Consider a rectangular Perspex beam of length 'L',breadth 'a' and thickness 'b'.A Plano convex lens is placed over the beam. Weight hanger is placed at both ends in which mass can be added. Knife edges were placed at a distance ‘l’ from both weight hangers. A light source is used to illuminate the arrangement.
THEORY

An air film is obtained between convex lens and Perspex beam. The light is made to fall normally on the air film with the help of a glass plate on the arrangement.
The interference fringes formed is viewed by means of travelling microscope. Without adding any mass in the weight hanger we get circular rings. But as we uniformly add mass on the weight hangers the beam bends and we get elliptical fringes.
During bending, an extension is caused on the upper surface and compression on the lower surface.
Let R1 be the longitudinal radius of curvature of the beam. The internal bending moment caused by extension of the surface above the bar and compression below the bar is given by
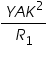
where ,
Y is the young’s modulus
A=ab, is the cross sectional area of bar
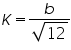 ,the radius of gyration for rectangular cross section.
,the radius of gyration for rectangular cross section.
In equilibrium condition the internal bending moment must be balanced by the moment due to weight m1g attached to its ends
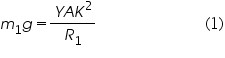
On rearranging we get, young’s modulus,
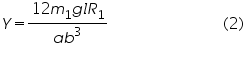
Also when the bar undergoes longitudinal bending, it also undergoes a lateral bending, resulting in lateral strain R2.
The ratio between these two quantities is the Poisson’s ratio and is given by

The longitudinal bending R1 can be found out using the equation,

where dn’ and dn are the diameters of nth ring with mass and without mass in longitudinal direction.
Similarly

where dn†and dn are the diameters of nth ring with mass and without mass in transverse direction.
So from the values of diameter of rings with mass and without mass, we calculate R1 and R2.
From those values of R1 and R2 we calculate young’s modulus 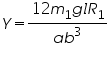
Poisson’s ratio,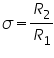 and bulk modulus,
and bulk modulus, 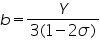





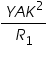
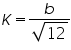 ,the radius of gyration for rectangular cross section.
,the radius of gyration for rectangular cross section.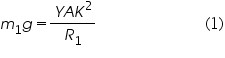
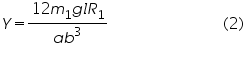




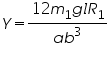
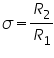 and bulk modulus,
and bulk modulus,