Procedure for doing Simulator
- Choose any desired environment by clicking on the ‘combo box’.
- Adjust the sliders to have suitable dimensions for flywheel arrangement.
- Click on ‘Release fly wheel’ to start the experiment.
- No of revolutions (N) of the flywheel, after the loop slips off from peg is indicated on the side of axle.
- The time taken by flywheel,t to come to rest is noted from stop watch.
- Repeat the experiment for different values of variables.
- From the value of N,t and variables find the value of moment inertia
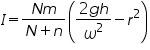
- Torque of flywheel is found using the equation
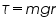 ,where m is the mass of weights added and r is the radius of axle.
,where m is the mass of weights added and r is the radius of axle.
- From the value of torque and inertia,the angular acceleration is found using equation,
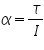
Procedure for doing Real Lab
- The length of the cord is carefully adjusted, so that when the weight-hanger just touches the ground,the loop slips off the peg.
- A suitable weight is placed in the weight hanger
- A chalk mark is made on the rim so that it is against the pointer when the weight hanger just touches the ground.
- The other end of the cord is loosely looped around the peg keeping the weight hanger just touching the ground.
- The flywheel is given a suitable number (n) of rotation so that the cord is wound round the axle without overlapping.
- The height (h) of the weight hanger from the ground is measured.
- The flywheel is released.
- The weight hanger descends and the flywheel rotates.
- The cord slips off from the peg when the weight hanger just touches the ground.By this time the flywheel would have made n rotations.
- A stop clock is started just when the weight hanger touches the ground.
- The time taken by the flywheel to come to a stop is determined as t seconds.
- The number of rotations (N) made by the flywheel during this interval is counted.
- The experiment is repeated by changing the value of n and m.
- From these values the moment of inertia of the flywheel is calculated using equation
![Double click to edit «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»I«/mi»«mo»=«/mo»«mfrac»«mrow»«mi»N«/mi»«mi»m«/mi»«/mrow»«mrow»«mi»N«/mi»«mo»+«/mo»«mi»n«/mi»«/mrow»«/mfrac»«mfenced close=¨]¨ open=¨[¨»«mrow»«mfrac»«mrow»«mn»2«/mn»«mi»g«/mi»«mi»h«/mi»«/mrow»«msup»«mi»§#969;«/mi»«mn»2«/mn»«/msup»«/mfrac»«mo»-«/mo»«msup»«mi»r«/mi»«mn»2«/mn»«/msup»«/mrow»«/mfenced»«/math»](/fckeditor/editor/plugins/fckeditor_wiris/integration/showimage.php?formula=ea35473201ef28ddb0b8151a13af1e35.png) .
.
Observations

Result
Angular acceleration of flywheel,α =........rads-2
Torque of flywheel,τ =..........rads-1




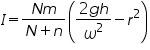
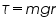 ,where m is the mass of weights added and r is the radius of axle.
,where m is the mass of weights added and r is the radius of axle.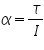
![Double click to edit «math xmlns=¨http://www.w3.org/1998/Math/MathML¨»«mi»I«/mi»«mo»=«/mo»«mfrac»«mrow»«mi»N«/mi»«mi»m«/mi»«/mrow»«mrow»«mi»N«/mi»«mo»+«/mo»«mi»n«/mi»«/mrow»«/mfrac»«mfenced close=¨]¨ open=¨[¨»«mrow»«mfrac»«mrow»«mn»2«/mn»«mi»g«/mi»«mi»h«/mi»«/mrow»«msup»«mi»§#969;«/mi»«mn»2«/mn»«/msup»«/mfrac»«mo»-«/mo»«msup»«mi»r«/mi»«mn»2«/mn»«/msup»«/mrow»«/mfenced»«/math»](/fckeditor/editor/plugins/fckeditor_wiris/integration/showimage.php?formula=ea35473201ef28ddb0b8151a13af1e35.png) .
.