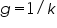| . | . | |||
| . | Bacterial Growth Curve |
. | ||
| . |
Objectives:
Principle:
Fig 1: Absorbance reading of bacterial suspension
The growth curve has four distinct phases (Fig 2)
1. Lag phaseWhen a microorganism is introduced into the fresh medium, it takes some time to adjust with the new environment. This phase is termed as Lag phase, in which cellular metabolism is accelerated, cells are increasing in size, but the bacteria are not able to replicate and therefore no increase in cell mass. The length of the lag phase depends directly on the previous growth condition of the organism. When the microorganism growing in a rich medium is inoculated into nutritionally poor medium, the organism will take more time to adapt with the new environment. The organism will start synthesising the necessary proteins, co-enzymes and vitamins needed for their growth and hence there will be a subsequent increase in the lag phase. Similarly when an organism from a nutritionally poor medium is added to a nutritionally rich medium, the organism can easily adapt to the environment, it can start the cell division without any delay, and therefore will have less lag phase it may be absent.
2. Exponential or Logarithmic (log) phaseDuring this phase, the microorganisms are in a rapidly growing and dividing state. Their metabolic activity increases and the organism begin the DNA replication by binary fission at a constant rate. The growth medium is exploited at the maximal rate, the culture reaches the maximum growth rate and the number of bacteria increases logarithmically (exponentially) and finally the single cell divide into two, which replicate into four, eight, sixteen, thirty two and so on (That is 20, 21, 22, 23.........2n, n is the number of generations) This will result in a balanced growth. The time taken by the bacteria to double in number during a specified time period is known as the generation time. The generation time tends to vary with different organisms. E.coli divides in every 20 minutes, hence its generation time is 20 minutes, and for Staphylococcus aureus it is 30 minutes.
3. Stationary phaseAs the bacterial population continues to grow, all the nutrients in the growth medium are used up by the microorganism for their rapid multiplication. This result in the accumulation of waste materials, toxic metabolites and inhibitory compounds such as antibiotics in the medium. This shifts the conditions of the medium such as pH and temperature, thereby creating an unfavourable environment for the bacterial growth. The reproduction rate will slow down, the cells undergoing division is equal to the number of cell death, and finally bacterium stops its division completely. The cell number is not increased and thus the growth rate is stabilised. If a cell taken from the stationary phase is introduced into a fresh medium, the cell can easily move on the exponential phase and is able to perform its metabolic activities as usual.
4. Decline or Death phaseThe depletion of nutrients and the subsequent accumulation of metabolic waste products and other toxic materials in the media will facilitates the bacterium to move on to the Death phase. During this, the bacterium completely loses its ability to reproduce. Individual bacteria begin to die due to the unfavourable conditions and the death is rapid and at uniform rate. The number of dead cells exceeds the number of live cells. Some organisms which can resist this condition can survive in the environment by producing endospores.
Fig 2: Different phases of growth of a bacteria CALCULATION:
Fig 3: Calculation of generation time
The exactly doubled points from the absorbance readings were taken and, the points were extrapolated to meet the respective time axis.
Let No = the initial population number
Therefore,
Therefore,
The growth rate can be expressed in terms of mean growth rate constant (k), the number of generations per unit time.
Therefore,
Substituting equation 4 in equation 3
Therefore,
Mean growth rate constant, Note:
|
..... | ||
| ..... | ..... | |||
 |
Copyright @ 2024 Under the NME ICT initiative of MHRD |
 |






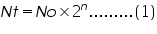
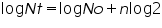
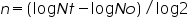
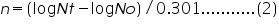
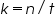
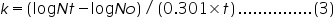

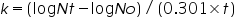
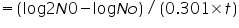
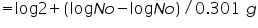 (Since the population doubles t= g)
(Since the population doubles t= g)