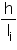Objective:

 

• To familiarise the 3D geometry of various molecules.
• To determine the point groups.

 

Introduction:

 

The symmetry relationships in the molecular structure provide the basis for a mathematical theory, called group theory. The mathematics of group theory is predominantly algebra. Since all molecules are certain geometrical entities, the group theory dealing with such molecules is also called as the ‘algebra of geometry’.

 

Symmetry Element:

 

A symmetry element is a geometrical entity such as a point, a line or a plane about which an inversion a rotation or a reflection is carried out in order to obtain an equivalent orientation.

 

Symmetry Operation:

 

A symmetry operation is a movement such as an inversion about a point, a rotation about a line or a reflection about a plane in order to get an equivalent orientation.

 

The various symmetry elements and symmetry operations are listed in below table.

 

Symmetry element	Symmetry operation	Schoenflies symbol	Hermann-Mauguin symbol
Centre of Symmetry or Inversion centre	inversion	I	ī
Plane of symmetry	Reflection θ	σ	m
Axis of symmetry	Rotation through	Cn	n
Improper axis	Rotation followed by reflection in a plane perpendicular to axis	Sn	ñ
Identity element	Identity Operation	E

 

Centre of symmetry:

A point in the molecule from which lines drawn to opposite directions will meet similar points at exactly same distance. Some of the molecules, which have a centre of symmetry, are:

N₂F_2, PtCl₄, C₂H₆

 

 

1,2-di chloro-1,2-di bromoethane(all trans and staggered)

 

Plane of symmetry:

 

A plane which divides the molecule into two equal halves such that one half is the exact mirror image of the other half. The molecules, which have plane of symmetry, are:

H₂O, N₂F_2, C₂H₄ 

 

  

 

The broken line in the σ- plane. If we look from left side (A) into the mirror plane, H_A appears to have gone on the other side and its image appears exactly at H_B. Similarly viewing the structure of H₂O molecule from the right side (B), the reflection of H_B appears at H_A configuration II is the result of this reflection operation and is equivalent to I. Another round of this operation on the molecule (configuration II) yields configuration III which is identical to configuration I.

 

Proper Axis of symmetry:

 

An axis passing through the molecule about which when the molecule is rotated 360/n an equivalent orientation is produced. This is an axis of n-fold symmetry or an axis of order as shown below.

H₂O, N₂H_3, BF₃

 

 

 

Initially, H₂O molecule is in configuration I, lying flat on the plane of the paper , and after rotating it through an angle θ = 180⁰ about an axis passing through O atom (Z-axis) and having HOH angle, the configuration II will be obtained. The configuration II is equivalent to configuration I, but not identical. By another similar rotation about Z-axis on configuration II, the molecule goes into configuration III. Here configuration III is identical to the initial or original configuration I. 

 

Principle Axis:

 

If there is more than one axis of symmetry, in many cases one of the axes is identified as principal axis, which will be selected in the following order:

 

• The only axis 
• The highest order axis
• The axis passing through maximum number of atoms
• The axis perpendicular to the plane of the molecule

 

The principal axis is taken as the vertical axis that is in the z-direction. The subsidiary axis is perpendicular to the principal axis and will, hence, be in the horizontal direction.

 

 

Molecule	Principal axis	Subsidiary axis
Water	C2	Nil
Ammonia	C3	Nil
BF3	C3	3C2
XeF4	C4	4C2
Cyclopentadienyl anion	C5	5C2
Benzene	C6	6C2
H2O2	C2	Nil
XeOF4	C4	Nill

 (a C_n  axis can combine with only n C₂ axis perpendicular to it or with no subsidiary axis.)

 

The plane of symmetry is also classified on the basis of the principal axis. The planes including or involving the principal axis are called vertical planes (σ_v) and the planes perpendicular to the principal axis is called horizontal plane (σ_h)_.

 

 

Molecule	Principal axis	Vertical planes	Horizontal planes
Water	C2	Nil	Nil
Ammonia	C3	Nil	One
BF3	C3	2	Nil
XeF4	C4	3	Nil
Cyclopentadienyl anion	C5	3	One
Benzene	C6	4	One
H2O2	C2	6	One
XeOF4	C4	4	Nil

 

 Improper Axis of symmetry:

 

An axis passing through the object about which when the object is rotated through 360/n followed by reflection in a plane perpendicular to the axis produces an equivalent orientation.

 

For example ethane molecule (staggered form).

 

 

Configuration I and II are not equivalent i.e., θ = 60⁰ and the consequence C₆ – rotational operation is not a valid symmetry operation by itself. Similarly, II and III are not equivalent, thus showing that σ operation perpendicular to the so called C₆ rotational axis is also not a genuine symmetry operation. But the configurations I and III are equivalent, so that C₆ followed by σ perpendicular to C₆ is a genuine, through the combined operation this product operation results in an element called S₆ axis.

 

Identity Element:

 

This element is obtained by an operation called identity operation. After this operation, the molecule remains as such. This situation can be visualized by two ways. Either

 

• We do not do anything on the molecule or
• We rotate the molecule by 360⁰.

 

 

 

Every molecule has this element of symmetry and it co-exists with the identity of the molecule, hence the name identity element.

 

Point group:

 

The symmetry elements can combine only in a limited number of ways and these combinations are called the point groups.

 

Nomenclature of the point group:

 

• There are certain conventions developed by two schools of thought for naming these point groups.
• The Schoenflies nomenclature is popularly used molecular point groups than that of Hermann-Mauguin.
• Crystal and space groups are named after Hermann-Mauguin symbolism.
• H₂O and pyridine are assigned the point group symbol-C_2v which means the molecules contain a C₂ axis and 2 σ_v planes.

 

Identification of molecular point groups:

 

The whole molecules are divided into three broad categories.

 

• Molecules of low symmetry (MLS).
• Molecules of high symmetry (MHS).
• Molecules of special symmetry (MSS).

 

Molecules of Low Symmetry (MLS):

 

The starting point could be the molecules containing no symmetry elements other than E, such molecules are unsymmetrically substituted and these molecules are said to be belongs to C₁ point group.

 

The TeCl₂Br₂ molecules with its structure in gaseous phase belongs to C₁ point group, and tetrahedral carbon and silicon compounds of the formula AHFClBr (A=C,Si).

 

 Molecules of High Symmetry (MHS):

 

In this category all the molecules containing C_n axis (invariably in the absence or presence of several other types of symmetry of elements) are considered. There are three main types of point groups C_n, D_n, and S_n.

 

 C_n type point group:

 

• C_n point groups:

 

The molecules which contain only one C_n, proper axis are considered. The presence of C_n implies the presence of (n-1) distinct symmetry elements whether n is even or odd. Since C_n generates a set of n elements including E, the order of this group is n, (h=n) the molecules belonging this group are designated as C_n point groups.

 

                                                                                                

 

• C_nv point groups:

 

This group contains a C_n axis and n σ_v planes of symmetry. When n is odd, all the planes are σ_v type only, and if n is even, there are n/2 planes of σ_v type and another n/2 planes of σ_v^’ type

   

• C_nh point groups:

 

This set of point group can by adding a horizontal plane (σ_h) to a proper rotational axis, C_n. This group has a total of 2n elements –n elements from C_n and other n elements can be generated by a combination of C_n and σ_h, leading to the corresponding S_n axes. When n is even, C_nh point group molecules necessarily contains a centre of inversion, i.

 

S-trans-1,3-Butadiene - C_2h            Boric acid - C_3h

 D_n type point groups:

 

• D_n point groups:

 

These are purely rotational groups that are they contain only rotational axis of symmetry. When the molecule containing only one type C_n axis, it was classified as C_n point group. if in addition to one the C_n  axis, a set of n C_n  axes perpendicular to C_n  are added, it belongs to another point group called D_n point group. The order, h, of this rotational group is 2n, since C_n generates (n-1)+E elements and the number of C_2s are n more. 

 

For example gauche or skew form of ethane contains D₃ point group.

 

  

 Biphenyl (skew) - D₂

 

• D_nh point groups:

 

This point group can be obtained by adding a horizontal (σ_h) plane to a set of D_n group elements. The order of this D_nh group is 4n. In addition to the n elements of C_n when n is even, the elements generated are quite distinct and different from what has already been obtained. However when n is odd, we get set of n elements based on S_n axis.

 

Example is -  B₂H₆ - D_2h

 

 

• D_nd point group:

 

This point group can be obtained by adding a set of dihedral planes (nσ_d) to a set of D_n group elements. This would thus require that there is a C_n proper axis along with nC₂ s perpendicular to C_n axis and nσ_d planes, constituting a total of 3n elements thus far.

 

Example is - Cyclohexane (chair form) - D_3d

 

             

S_n type point groups:

 

S_n axis is the only group generator for the S_n (n= even) point group of molecules. The point groups C_nh, D_nh, and D_nd .when n is odd, the presence of S_n axis implies the presence of 2n elements, in which a plane of symmetry (σ) makes an independent appearance. Thus the presence of a plane perpendicular to C_n or S_n axis and other additional elements would lead to the other point group such as C_nh , D_nh ,or D_nd when n is even and there is no plane perpendicular (σ_h ) to this axis, the presence of other elements in addition to S_n axis leads to only D_nd point group.

 

Example is - SiO₄(CH₃)₄ - S₄

 

 Point Groups and their Detailed List of Symmetry  Elements are Included in the Below Table.

 

Point group	Order of group, h	Type of symmetry elements
C1	1	E (=C1)
C1	2	E, I (=S2 )
C1	2	E, σ
Cn – groups: ( h = n )
C2	2	E, C2
C3	3	E C31, C32
C4	4	E, C41, C42 (=C2), C43
C5	5	E, C41, C42 ,C43, C44
Cnv – groups: ( h = 2n )
C2v	4	E, C2 , σ
C3v	6	E,C31, C32 , 3σv
C4v	8	E,C41,C42(=C2), C43, 2σv, 2σv’
Cnh – groups: ( h = 2n )
C2h	4	E, C2 ,i=( S2 ), σh
C3h	6	E, C31, C32 , S31, S35, σh
C4h	8	E,C41,C42(=C2), C43, S41, S43,σh, i=( S2 )
Dn – groups: ( h = 2n )
D2	4	E, C2, C2’
D3	6	E, C31, C32, 3C2
D4	8	E,2C4, C2, 4C2
Dnh – groups: ( h = 4n )
D2h	8	E, C2 , 2C2’ , i=( S2 ), σh , 2σv
D3h	12	E, 2C3 ,3C2 , σh ,3σv , 2S3, (S31, S35)
D4h	16	E, 2C4,( C41,C42 ), C2=( C42), 2C2’ ,2C2”, σh ,2σv ,3σd, i , 2S4 (S41, S43 )
Dnd– groups: ( h = 4n )
D2d	8	E, C2 , 2C2’, 2 σd, 2S4
D3d	12	E, 2C3 (C31, C32), 3C2 ,i, 3σd, 2S6(S61, S63 )
D4d	16	E, 2C4, (C41, C43), C2=( C42),  4C2’ ,4σd, 4S8(S81, S83 , S85, S87)
Sn (n=even)– groups: ( h = n )
S4	4	E, S41, S43 , C2
S6	6	E, S61, S45, C31, C32, i
S8	8	E, S8 ,S81, S83 , S85, S87, C41, C43, C2=( C42)
Infinite- point group (h=∞)
C∞v	∞	E, ∞, C∞, ∞σv
D∞v	∞	E, ∞, C∞, ∞σv, σh, i

 

Molecules of special Symmetry:

 

This class has two groups of molecules:

 

• Linear or infinite groups and
• Groups which contain multiple higher-order axes.

 

• Linear or infinite groups:

In addition to all the linear molecules, circle-shaped and cone-shaped ones also belong to this category. These can be further sub-divided into two groups, C_∞v and D_∞v groups, the presence or absence of i used to distinguish between these two types of groups.

 

• C_∞v point group:

This group can be defined the same way as that of C_nv group, where n is infinity. The C_∞ axis lies along the inter nuclear molecules, and since the molecule is linear the σ_v planes are infinite in number. The order of this group is h = ∞. All hetero nuclear molecules, and all unsymmetrically substituted linear polyatomic molecules are belongs to this point group.

 

Examples are HX (X = F, Cl, Br, I), CO, NO, CN etc. 

 

• D_∞v point group:

This group is an extension of D_nh group (∞). This group of molecules contain a C_∞ axis, ∞C₂ axes perpendicular to C_∞ axis and a σ_h plane. Then, it would also imply that the molecule possess ∞σ_v planes and a centre of inversion(i). So all centre of symmetric molecules are belongs to this point group.

 

                   Homo nuclear diatomic molecules such as N₂, O₂ , H₂ , F₂  and Cl₂ etc.

 

Molecules Containing Multiple Higher-Order Axes:

 

This is a special class of molecules which contain more than one type of rotational axes (n≥2) that are neither perpendicular to the principal C_n axis (n-highest), as in D_n and related point groups, nor bear any perpendicular relationship. These high-symmetry molecules have shapes corresponding to the five platonic solids: tetrahedral, octahedral, cube, dodecahedral and icosahedra.

 

Tetrahedral Point Groups:

 

The highest-fold axis in these point groups is C₃ axis, which is occur in multiples. Molecules with only C₃ axes and additionally only C₂ axes belong to T, a pure rotational point group, since they contain only proper rotational axes. All other type of elements (σ_v ,i, S_n) are absent in three groups.

T:   8C₃ (4C₃¹, 4C₃²), 3C ₂, E   

                                                                   

        Si(CH₃)₄

When σ_d, S₄ (collinear with C₂ axes) elements are added to the T group elements, we get a full group called T_d. The order of this group is 24.

 

T_d: 8C₃ (4C₃¹, 4C₃²), 3C ₂, E, 6S₄ (S₄¹, S₄³), 6 σ_d

 

   CCl₄ 

 

There is another uncommon point group, T_h, which can be obtained by adding three planes of symmetry (σ_h) to T group. The order of this is group is 24.

 

T_h :8C₃ (4C₃¹, 4C₃²), 3C ₂, i, 3σ_h, 8S₆ (4S₆¹, 4S₆⁵)

 

Example - Co(NO₂)₆^3-

 

 

 

Octahedral Point Groups:

 

This is another class of cubic groups. Additionally, octahedral point groups have multiple C₄ axes when compared to that of tetrahedral groups.

 

When the group contains only rotational axes, it is labelled as O group, h, of this group are 24.

 

O:    E, 6C₄ (3C₄¹, 3C₄²), 8C₃ (4C₃¹, 4C₃²), 6C ₂, 3C ₂ ‘=3C₄²

 

To the O group elements, if 3σ_h and 6 σ_d planes are added, a group of higher symmetry can be generated. The order of this group is 48. 

 

O_h  E, 6C₄ (3C₄¹, 3C₄²), 3C ₂ ‘=3C₄², 6C ₂, 8C₃ (4C₃¹, 4C₃²), i, 3σ_h, 6σ_d, 6S₄ (S₄¹, S₄³), 8S₆ (4S₆¹, 4S₆⁵)

 

  

Cubane

 

Icosahedral Groups:

 

This group contains molecules with either icosahedral or pentagonal dodecahedral shapes and belongs to I_h point groups. The molecules containing only the rotational elements are said to be belongs to I point group. The order of this point group is 60, whereas that full group is 120.

 

I        E, 24C₅ (6C₅¹, 6C₅², 6C₅³, 6C₅⁴), 20C₃ (10C₃¹, 10C₃²), 15C ₂

I_h       E, 24C₅, 20C₃, 15C ₂,24S₁₀ (6S₁₀¹, 6S₁₀³6S₁₀⁷,6S₁₀⁹), 20S₆ (10S₆¹, 10S₆⁵), i, 15σ

 

Fullerene 

 

Great Orthogonality Theorem:

 

The matrices of the different Irreducible Representations (IR) possess certain well defined interrelationships and properties. Orthogonality theorem is concerned with the elements of the matrices which constitute the IR of a group.
 

The mathematical statement of this theorem is,

 

 

Where,

 

i, j – Irreducible Representations

 

l_i, l_j – Its dimensions

 

h – Order of a group

 

Γ_i(R)_mn – Element of m^th row, n^th column of an i^th representation

 

Γ_j(R)'m'n' - Element of m' ^th row, n' ^th column of j' ^th representation

 

δ_ij δ_mm' δ_nn' – Kronecker delta

 

Kronecker delta can have values 0 and 1. Depending on that the main theorem can be made into three similar equations.

 

i.e.,

1. When, Γ_i ≠ Γ_j and j ≠ i, then δ_ij = 0

 

Therefore, Σ_R [ Γ_i(R)_mn ] [ Γ_j(R)'m'n' ]^* = 0

 

2. When, Γ_i = Γ_j and j = i, then δ_ij = 1

 

Therefore, Σ_R [ Γ_i(R)_mn ] [ Γ_i(R)'m'n' ]^* = 0

 

From these two equations we can say the Orthogonality theorem as, “the sum of the product of the irreducible representation is equal to zero”.

 

3. When i = j, m = m', n = n'

 

Then, Σ_R [ Γ_i(R)_mn ] [ Γ_i(R) mn]^* = 

 

From the above equations some important rules of the irreducible representations of a group and there character were obtained.

 

 

Five Rules Obtained:

 

1. The sum of the squares of the dimensions of the representation = the order (h) of the group.

 

i.e., Σ_li² = l₁² + l₂² + l₃² + …… l_n² = h

 

Γ_i(E) –the character of the representation of E in the ith IR which is equal to the dimension of the representation.

 

i.e., Σ_i [ Γ_i(E)]² = h

 

2. The sum of the squares of the characters in any IR is equal to ‘h’.

 

i.e., Σ_R [ Γ_i(R)]² = h

 

3. The vectors whose components are the characters of two different IR are orthogonal.

 

i.e., Σ_R Γ_i(R) Γ_j(R) = 0 when i ≠ j.

 

4. In a given representation (reducible/irreducible) the characters of all matrices belonging to operations in the same class are identical.

 

Eg:- in C_3v point group there are, E, 2C₃, 3 σ_v. there characters are same for a particular IR.

 

5. No: of irreducible representation in a group = No: of classes in a group.

 

Applications:

 

Applying these 5 rules we can develop the character table for various point groups. For most chemical applications, it is sufficient to know only the characters of the each of the symmetry classes of a group.

 

Steps for The Construction of A Character Table::

 

1. Write down all the symmetry operations of the point group and group them into classes.
2. Note that the no: of the IR is found out using the theorem.
3. Interrelationships of various group operations are to be carefully followed.
4. Use the orthogonality and the normality theorem in fixing the characters.
5. Generate a representation using certain basic vectors. Try out with X, Y, Z, R_σ, R_y, R_z etc. as the bases and check.

 

Character Table for C_2v Point Group:

 

1. For C_2v point group, there are 4 symmetry operations, Γ₁, Γ₂, Γ₃, Γ₄ therefore, it contains 4 classes. i.e., E, C_2z, σ_xz, σ_yz. And character of E is denoted as l₁, l₂, l₃, l₄.

 

C2v	E	C2z	σxz	σyz
Γ1	l1
Γ2	l2
Γ3	l3
Γ4	l4

 

2. The sum of the squares of the dimensions of the symmetry operations = 4.

 

i.e., l₁² + l₂² + l₃² + l₄² = h = 4.

 

This can only be satisfied by four one dimensional representations.

 

C2v	E	C2z	σxz	σyz
Γ1	1
Γ2	1
Γ3	1
Γ4	1

 

The unknowns for Γ₁ is a₁, b₁, c₁ , for Γ₂ is a₂, b₂, c₂.

 

C2v	E	C2z	σxz	σyz
Γ1	1	a1	b1	c1
Γ2	1	a2	b2	c2
Γ3	1	a3	b3	c3
Γ4	1	a4	b4	c4

 

3. Sum of the squares of the characters of any IR is equal to the order of the group.

 

i.e., 1² + a₁² + b₁² + c₁² = 4.

 

C2v	E	C2z	σxz	σyz
Γ1	1	1	1	1
Γ2	1	a2	b2	c2
Γ3	1	a3	b3	c3
Γ4	1	a4	b4	c4

 

4. The orthogonality theorem must be satisfied by all the symmetry operations. 

 

i.e., Σ_R Γ_i(R) Γ_j(R) = 0

i.e., for Γ₁ . Γ₂

i.e., 1.1 + a₁ .1 + b₂ . 1 + c₂ .1 = 0

Let a₂ = 1, b₂ = -1 and c₂ = -1

Then Γ₁ . Γ₂ = 0

 

 

C2v	E	C2z	σxz	σyz
Γ1	1	1	1	1
Γ2	1	1	-1	-1
Γ3	1	a3	b3	c3
Γ4	1	a4	b4	c4

 

For Γ₃ . Γ₁

i.e., 1.1 + a₃ .1 + b₃ . 1 + c₃ .1 = 0

Let a₃ = -1, b₃ = 1 and c₃ = -1

Then Γ₁ . Γ₂ = 0

 

 

C2v	E	C2z	σxz	σyz
Γ1	1	1	1	1
Γ2	1	1	-1	-1
Γ3	1	-1	1	-1
Γ4	1	a4	b4	c4

 

For Γ₄ . Γ₁

i.e., 1.1 + a₄ .1 + b₄ . 1 + c₄ .1 = 0

Let a₄ = -1, b₄ = -1 and c₄ = 1

Then Γ₁ . Γ₂ = 0

 

 

C2v	E	C2z	σxz	σyz
Γ1	1	1	1	1
Γ2	1	1	-1	-1
Γ3	1	-1	1	-1
Γ4	1	-1	1	-1

 

Rules For Assigning Mullicon Symbols:

 

1. If the IR is unidimensional term A or B is used.

If it is two dimensional E is used.

If it is three dimensional T is used.

 

2. If one dimensional IR is symmetric with respect to the principle axis C_n, i.e., character of C_n is +1, the term A is used. If it is -1, the term B is used.

 

3. If IR is symmetric with respect to subsidiary axes then subscript 1 is given and is antisymmetric then subscript 2 is given.

 

4. Prime and double prime marks are used for indicating symmetric or antisymmetric with respect to horizontal plane.

 

5. ‘g’ and ‘u’ subscripts are given for those which are symmetric and antisymmetric respectively with respect to centre of symmetry then,

 

 

C2v	E	C2z	σxz	σyz
A1	1	1	1	1
A2	1	1	-1	-1
B3	1	-1	1	-1
B4	1	-1	1	-1

 

In any character table there are 4 different areas.

 

Area I              – Characters of symmetry operations

Area II             – Mullicon Symbols

Area III            – Cartesion coordinates of rotation axes.

Area IV            – Binary Products

 

Area III:

 

In order to assign the cartesion coordinates, different operations are performed on each of the axes. Here we find the symbols X, Y, Z represents coordinates and rotations R_x, R_y and R_z.

 

 

Similarly,

 

 

 

The characters are 1 -1 1 -1 corresponding to B₁. And with respect to vector Y, 1 -1 -1 1 and therefore corresponds to B₂. Similar arrangement could be made to rotation axes Rx, Ry, Rz representing rotation about XZ axes. In order to see how they transformed, a curved arrow should be considered around the axes. If the direction of the head of the curved arrow doesn’t change due to operation, the character is +1, otherways it is -1.

 

 

 

The characters are 1 1 -1 -1. Therefore it will be A₂ and it becomes Rz.

 

 

 

The characters are 1 -1 1 -1. Therefore it will be B₁ and it becomes R_x. Similarly B₂ become R_y.

 

Therefore,

 

C2v	E	C2z	σxz	σyz	Linear Functions, Rotations
A1	1	1	1	1	Z
A2	1	1	-1	-1	Rz
B1	1	-1	1	-1	X, Ry
B2	1	-1	-1	1	Y, Rx

 

Area IV:

 

Which represents the squares and binary products.

 

A₁         = Z       = 1 1 1 1

A₁²       = Z²     = 1 1 1 1          = A₁

B₁         = X       = 1 -1 1 -1

B₁²       = X²     = 1 1 1 1          = A₁

B₂         = Y       = 1 -1 -1 1

B₂²       = Y²      = 1 1 1 1          = A₁

XY        = B₁ . B₂           = 1 1 -1 -1        = A₂

XZ        = B₁ . A₁           = 1 -1 1 -1        = B₁

YZ        = B₂ . A₁           = 1 -1 -1 1        = B₂

 

Therefore the actual character table for C_2v point group will be,

 

C2v	E	C2z	σxz	σyz	Linear Functions, Rotations	Quadratic
A1	1	1	1	1	Z	X2, Y2, Z2
A2	1	1	-1	-1	Rz	XY
B1	1	-1	1	-1	X, Ry	XZ
B2	1	-1	-1	1	Y, Rx	YZ

 

Character Table for C_3v Point Group:

 

1. For C_3v point group, there are 6 symmetry operations and 3 classes, i.e., Γ₁, Γ₂, Γ₃.

 

2. The sum of the squares of the dimensions of the symmetry operations = 6.

 

i.e., l₁² + l₂² + l₃² = h = 6.

 

This can only be satisfied by, 2 one dimensional and 1 two dimensional representations.

 

C3v	E	2C3	3σv
Γ1	1	a1	b1
Γ2	1	a2	b2
Γ3	2	a3	b3

 

3. The sum of the dimensions of Γ₁ also 6.

 

Therefore, its characters are (1 1 1).

 

 

C3v	E	2C3	3σv
Γ1	1	1	1
Γ2	1	a2	b2
Γ3	2	a3	b3

 

4. All operations must satisfy the orthogonality condition, Σ_R Γ_i (R) Γ_j (R) = 0

 

i.e., For Γ₁ . Γ₂

i.e., 1.1 + 2 . a₂ .1 + 3 . b₂ . 1 = 0

Let a₂ = 1 and b₂ = -1

Then Γ₁ . Γ₂ = 0

 

 

C3v	E	2C3	3σv
Γ1	1	1	1
Γ2	1	1	-1
Γ3	2	a3	b3

 

i.e., For Γ₃ . Γ₂

i.e., 2.1 + 2 . a₃ .1 - 3 . b₃ . 1 = 0

Let a₃ = -1 and b₃ = 0

Then Γ₃ . Γ₂ = 0

 

 

C3v	E	2C3	3σv
Γ1	1	1	1
Γ2	1	1	-1
Γ3	2	-1	0

 

For any character table there are 4 areas.

 

For Area I:

 

Assign the Mullicon symbols.

 

 

C3v	E	2C3	3σv
A1	1	1	1
A2	1	1	-1
B	2	-1	0

 

For Area III:

 

In order to assign the Cartesian coordinates different operations are performed on each of the axes. Here we were finding the symbols X, Y, Z represents coordinates and rotations R_x, R_y and R_z.

 

Consider,

 

 

The characters are 1 1 1 corresponding to A₁.

 

 

The characters are 1 -1 1, the character corresponding to C₃ will be -1. Therefore it will be E. Similarly for vector Y, we get 1 -1 1 and this also E.

 

Similar arrangement could be made to rotation axes R_x, R_y, R_z.

 

 

The characters are 1 -1 1. Therefore it corresponds to E and it will become R_x.

 

 

The characters are 1 1 -1. Therefore it corresponds to A₂ and it will become R_z.

 

Similarly for E the characters are 2 -1 0 and it will become R_y.

 

C3v	E	2C3	3σv	Linear Functions, Rotations
A1	1	1	1	Z
A2	1	1	-1	Rz
E	2	-1	0	(X, Y) (Rx, Ry)

 

Area IV:

 

Which represents the squares and binary products.

 

A₁         = Z                   = 1 1 1

A₁²       = Z²                 = 1 1 1             = A₁

XY        = E                   = 2 -1 0            = E

XZ        = E . A₁             = 2 -1 0            = E

YZ        = E . A₁             = 2 -1 0            = E

 

Therefore the actual character table for C_3v point group will be,

 

C3v	E	2C3	3σv	Linear Functions, Rotations	Quadratic
A1	1	1	1	Z	Z2
A2	1	1	-1	Rz
E	2	-1	0	(X, Y) (Rx, Ry)	(XY), (XZ), (YZ)

 

Some Important Character Tables for Molecular Point Groups:

 

1. Character Table for Non Axial Point Groups:
2. Character Table for C_n Point Groups:
3. Character Table for C_nv Point Groups:
4. Character Table for C_nh Point Groups:
5. Character Table for D_n Point Groups:
6. Character Table for D_nh Point Groups:
7. Character Table for D_nd Point Groups:
8. Character Table for S_n Point Groups:
9. Character Tables for Higher Point Groups:
10. Character Tables for Linear Point Groups:
11. 45